Как найти диагональ фундамента: выравнивание величины прямоугольника и расчет разметки

выравнивание величины прямоугольника и расчет разметки

После окончания проектирования размеры опоры строения переносятся на участок строительства. От качественной разметки зависит равномерность фундамента и правильное выставление отметок для возведения постройки. Чтобы сделать углы точно под 90°, проверяют диагонали фундамента и сравнивают их между собой. Если все сделано правильно, надземная часть будет прочной и не деформируется со временем.

Содержание

1. Необходимость расчета диагонали фундамента
2. Сложности при неправильной разметке
3. Правильный расчет диагонали фундамента
4. Необходимые инструменты для работы
5. Выравнивание величины прямоугольника
6. Нахождение третьего и четвертого углов

Необходимость расчета диагонали фундамента

При неверном расчете диагонали все дальнейшее строительство будет расходиться с планом

Проект предполагает подбор конструктивных элементов точно в размер, чтобы при строительстве не возникало перекосов. Длина балки или плиты перекрытия берется с требуемой глубиной опирания, которая принимается по конструктивному расчету. Во время разметки фундамента нужна предельная точность, т.к. отклонение в размерах повлечет расхождение вертикальных конструкций.

Горизонтальные элементы могут не влезть в проектное положение или вываливаться из монтажного пространства, поэтому потребуется перерасчет длины, а также других показателей.

Правильная разметка основания ведет к приятным бонусам при возведении здания:

• простота строительства стен и применения сборных элементов;
• соблюдение предусмотренной проектом экономии средств и материалов;
• сооружение объекта без отклонений от проекта;
• соответствие фактических размеров, периметра, ширины.

Перед тем как вымерить диагональ фундамента, нужно выровнять строительную площадку, чтобы удобно было размечать линии на местности. Почти всегда строительные конструкции и материалы от утеплительных матов до досок и стеновых щитов имеют прямые углы, поэтому фундамент также размечают с учетом этих требований.

Если диагонали прямоугольника оказываются равными, геодезист выполнил идеальную разметку. Если разметка не совпадает, спроектирован не прямоугольник. Но у равнобедренной трапеции также получаются диагонали одинаковой длины, поэтому проверяют стороны угла по принципу золотого сечения с помощью длинного шнура и рулетки.

Сложности при неправильной разметке

Нарушение геометрии фундамента снижает прочность стен

Неправильная переноска размеров на местность и пренебрежение сравнением диагоналей приведет к тому, что на поверхности земли появится ромб или трапеция. При устройстве самого столбчатого, свайного или плитного фундамента это может и не станет заметно, но первая укладка плит над подвалом выявит несоответствия и приведет к потерям времени для перерасчета сборных элементов или переделке основания.

Если плита опирается меньше требуемой глубины, после получения нагрузки от оборудования или людей она может обломить опорную часть стены и упасть. Такая неприятность коснется горизонтальных элементов перекрытия на всех этажах высотного строения и будет повторяться вплоть до кровли.

Выполнить устройство крыши трудно, если не соответствуют размеры между балками, фермы приходится ставить большего размера, а в других местах уменьшать габариты. Увеличивается трудоемкость работ, т.к. исполнитель выступает в несвойственной для него роли конструктора и проектировщика.

Усложнится установка кровельного покрытия, т.к. листы профнастила или шифера выпускаются с прямыми углами. Сборные угловые элементы водоотлива также рассчитаны на установку под 90°, желоб будет отходить от края кровли, а вода попадет на вертикальные ограждения, стены будут отсыревать.

Сложности возникнут с последующими работами, поэтому нужно проверить диагональ фундамента и сравнить результаты. Аналогично проводят измерения после установки опалубки, чтобы подтвердить правильность расчетов.

Правильный расчет диагонали фундамента

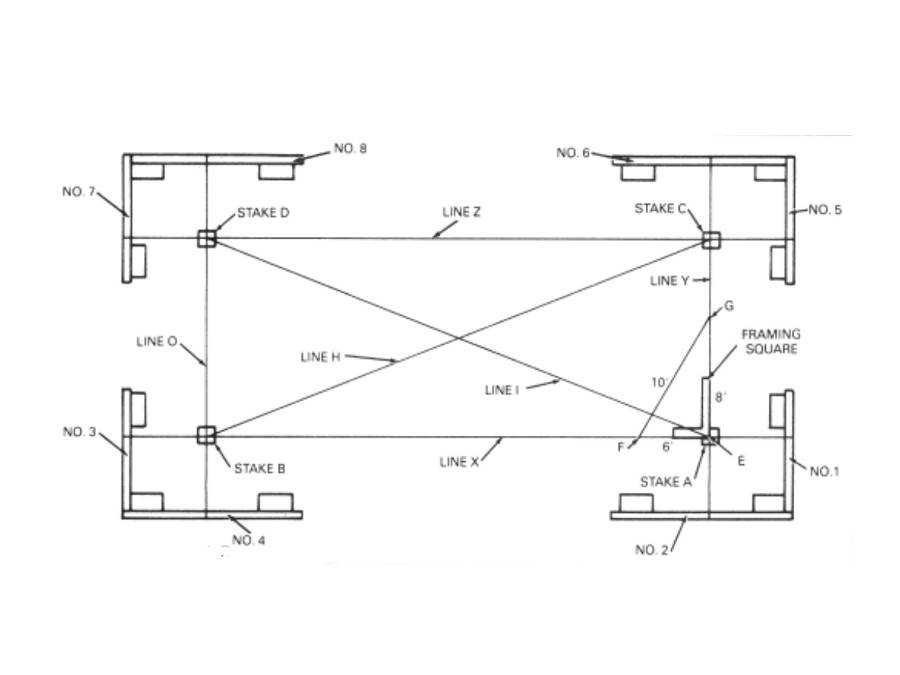
После изучения плана основания нужно приступать к разметке одной из сторон.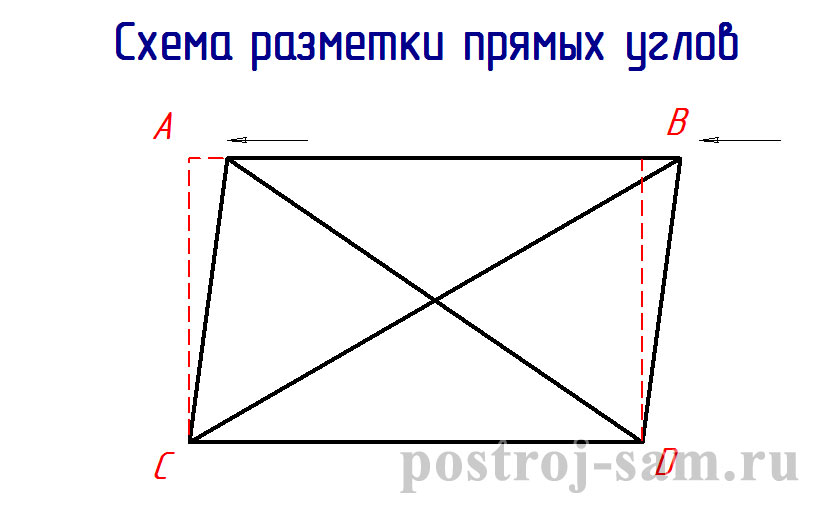 Это может быть боковая часть, фасадная или задняя, в данном случае это не является важным условием, т.к. принимается во внимание только ориентирование направления.

Длина фундаментной стены не учитывается, можно взять на 1,0 метр больше от места предстоящих углов. В этих точках забивают колья, и натягивают шпагат. Запас по длине дается, чтобы при копке траншеи не вытащить колышек, и он остался для обозначения направления стороны.

Колышки заменяют доской длиной 1 – 2 метра с прибитыми кольями в торце. Привязанный к ним шнур можно оперативно передвигать из стороны в сторону при необходимости. Такое приспособление для работы называют обноской, оно позволяет расчертить участок с точностью до нескольких миллиметров.

Порядок работы выполнения замеров:

• После натяжки шпагата находят точку отсчета по длине и определяют угол фундамента, на шпагате в этой точке цепляют прищепку или забивают кол в грунт, так появляется 2 угла.
• Идентично поступают с перпендикулярной стороной и определяют направление.
• Перед тем как рассчитать диагональ прямоугольного треугольника, по сторонам откладывают 3 и 4 равные части, отмечают их на шпагате (например, 3 и 4 метра).
• Зависимость расстояния между отмеченными точками такова, что гипотенуза должна быть равна пяти частям (5 метров) и не отличаться даже сантиметром, иначе пойдет скос.

Сразу трудно получить правильный результат разметки. Расстояние меньше пяти частей будет означать острый угол, а больше — говорить о величине, превышающей 90°.

Необходимые инструменты для работы

Инструменты для разметки фундамента

Во время рытья траншей экскаватором убирают шнуры, которые натянуты с выносом от углов, а места сторон отмечают на грунте посыпкой контрастным веществом, например, светлым песком или мелом. Элементы обноски красят яркой краской, чтобы экскаваторщик мог их увидеть и не наехать на разметочные части. После рытья траншеи шнуры натягивают на старое место и проверяют расположение ям или котлованов.

Расчет диагонали фундамента ведется с применением инструментов и приспособлений:

• колья из древесины или ровной арматуры, без кривизны;
• ровные куски металлического профиля или сухой рейки по 2 – 2,5 метра для горизонтального переноса точек;
• капроновый шнур или крепкий шпагат;
• гвозди, шурупы или саморезы;
• угольник, рулетка, молоток, ножницы;
• отвес, водяной или лазерный уровень.

Геодезисты используют теодолит, чтобы размечать углы и давать отметки по высоте. У частников нет такого инструмента, для работы с ним требуется навык.

На угольник закрепляют лазерные указки и строительный уровень — такое приспособление покажет высокую точность при разметке. Продаются транспортиры и угольники большого размера, лучше взять такие, чтобы было удобнее переносить линии плана на местность. Первоначальная разметка очень важна для начала строительства, поэтому желательно высчитать диагональ несколько раз, чтобы быть уверенным в правильности работы.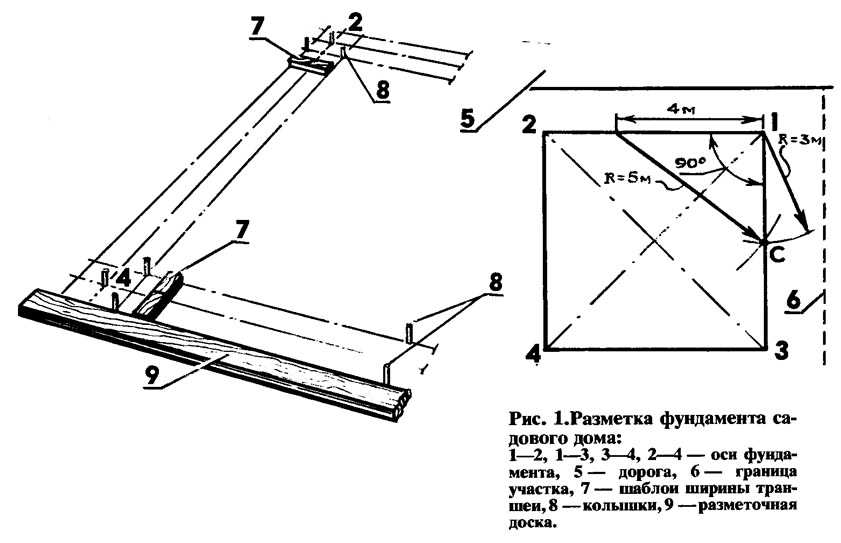

Выравнивание величины прямоугольника

Разбивка фундамента на прямоугольники

В прямоугольнике все углы должны равняться 90°, иначе получится неравнобедренная фигура с перекосами стен. Абрис фундамента имеет наружную и внутреннюю сторону, поэтому требование к прямоугольности касается обоих контуров. Легче всего выровнять величину для дома простой прямоугольной формы, который имеет четыре стены.

Иногда фундаменты в плане имеют сложное строение, например, делаются дополнительные монолитные ленты под пристройку или веранду, а каминный зал рассматривается как вынесенное помещение. В таком случае разметка усложняется тем, что площадь дома будет складываться из отдельных прямоугольников, которые размечаются отдельно.

Каждая фигура после распланировки поверяется на соответствие с другими частями и между составными элементами также устанавливаются прямые углы. Первоначальная сторона привязывается к какой-нибудь основе на местности, которая выглядит прямолинейно. Это может быть ограда, забор, трамвайные пути или бордюр асфальтированной трассы. От этой линии откладывается одинаковое расстояние для обозначения первой стороны искомого плана фундамента.

После окончательной разметки нужно правильно рассчитать разметку и сравнить расстояние между первой-третьей и второй-четвертой вершиной прямоугольника на местности. Должны получиться идеально одинаковые расстояния. Проверяют и длину противоположных сторон, которые также должны быть равны.

Нахождение третьего и четвертого углов

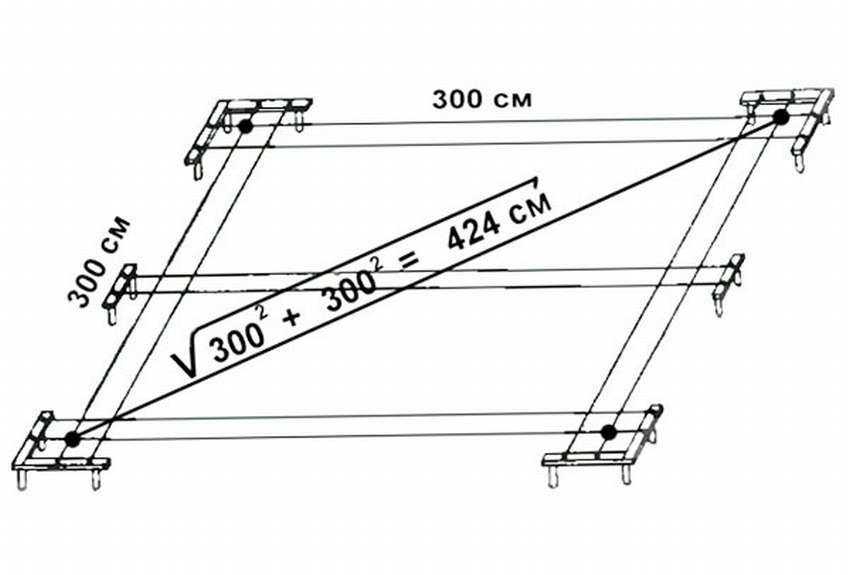
При расчете используется теорема Пифагора

Соответствие частей в треугольнике, по которому размечается прямой угол на участке, можно проверить теоремой Пифагора. Она выражается формулой a² + b² = c²: квадрат гипотенузы равняется сумме квадратов катетов.

Чтобы высчитать длину соединяющей гипотенузы, нужно высчитать квадрат одного расстояния на шнуре с квадратом другой стороны угла и сложить полученные значения. Из результата следует высчитать квадратный корень, чтобы получить длину гипотенузы. Так можно выровнять диагональ прямоугольника, чтобы получить идеальный прямой угол.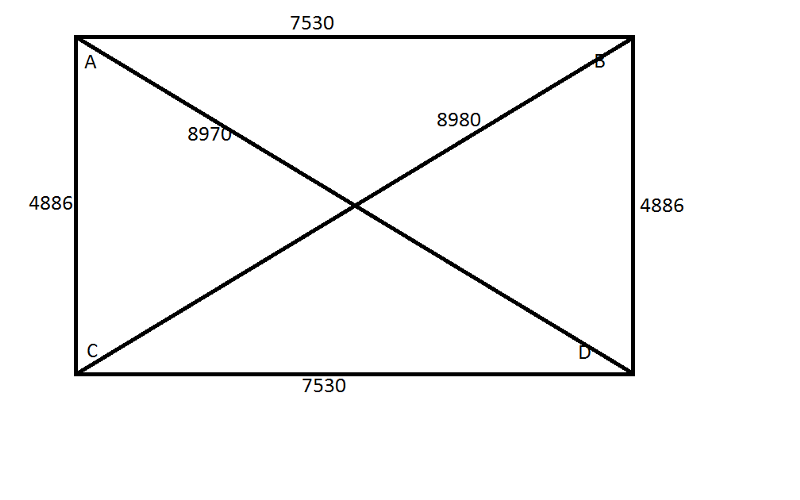

Третий и четвертый углы находятся аналогичным способом по отправной вершине и существующей стороне. После выставления последнего угла проверяется противоположные диагонали и стороны в фигуре для сравнения. Используется шнур, который не растягивается по длине, чтобы не искажать измерения.

Старинный способ измерить диагональ дома предполагает использование бечевки с завязанными на ней 13 узелками на абсолютно равном расстоянии друг от друга. На одну сторону прямоугольника приходилось 3 расстояния между узлами, при этом четвертый совпадал с вершиной угла. После верхушки отмеряли 4 таких отрезка. На гипотенузу приходилось оставшихся 5 промежутков, и первый узел при натяжении должен был совпадать с 13 завязанным элементом.

Разметка фундамента

Поскольку фундамент является важнейшей частью здания, правильное выполнение его разметки крайне необходимо. Будут обеспечены такие показатели, как достаточная прочность и устойчивость, при этом обеспечивается нужное распределение нагрузки.

Инструменты для выполнения разметки

Работы проводятся с использованием инструмента, позволяющего качественно и быстро выполнить задачу:

• уровень;
• отвес;
• рулетка;
• лазерные инструменты – нивелир, дальномер;
• шнур.

Дополнительно используются деревянные колья и обрезки арматуры.

Особенности выбора участка

Работы начинаются с выбора участка, который определяется по следующим критериям:

• перспективы проведения коммуникаций;
• состояние дорожной сети;
• географическая привязка к сторонам света.

Основным назначением разметки является создание правильной ориентации, применительно к местности, что позволит построить здание с учётом общепринятых технологических решений.

Процесс разметки фундамента

Работа будет проводиться в несколько этапов.

Первоначально осуществляется выявление угловых крайних точек – выявляются размеры объекта на местности. Любое здание традиционно привязывается к габаритам, причём не только угловым, но и линейным. Также существует привязка к геодезическим опорам, отмеченным в проектировочной разбивочной схеме. Требуется добиться верного расположения стен, которые должны быть параллельны границам участка. Определяются и фиксируются крайние точки стены, для чего используется лазерный дальномер и колья из дерева.

Начальной точкой является угол первой конструкции, от которого откладывается нужная длина. Чтобы рассчитать прямоугольный угол, необходимо найти диагональ, прибегнув к теореме Пифагора. Третий колышек, устанавливается в месте пересечения двух предыдущих кольев. Идентичный принцип используется при установке четвёртого колышка. Последовательность выполнения разметки будет следующей:

• первая стена:
• вторая стена – выбираем в качестве исходной точки угол первой;
• расчёт диагонали угла;
• выявление точек 3 и 4;
• границы отмечаются при помощи канатов.

Так же смотрите:

1. Строительство фундамента зимой
2. Ленточный фундамент для дома

 

Начинается работа по выкапыванию котлована, для чего в каждом из углов устанавливаются колья, являющиеся ориентиром. Используя колья, натягивают шпагат вдоль всего периметра будущего здания. После этого надо выяснить, каковым является горизонтальный уровень каждой из стен, для чего пользуются специализированными приспособлениями:

• лазерный дальномер;
• гидроуровень;
• нивелир.

Определив нужные параметры, следует выполнить на кольях точную разметку, наносимую на одном уровне, при этом оптимальной высотой считается расстояние 30см. Когда измерения проведены, приступают к рытью траншеи, ориентируясь на метки в качестве точек, от которых отмеряют глубину, указанную в проектных документах.
Выполняя разметку котлована, надо учитывать, что его габариты должны на 0. 5 метра превышать фундаментальное основание дома. Необходимо учесть, что если в процессе рытья используется техника, то необходимо осуществлять контроль глубины, что своевременно нивелировать отклонения от нормы. Используют для этих целей лазерный уровень. Когда этап завершён, следует натянуть шпагаты, пересечения которых переносится на дно, для чего вбивают колья и пользуются отвесом.

Особенности разметки фундамента

Размечая фундамент необходимо учитывать ряд особенностей, которые необходимо в строгости соблюдать:

• идеально прямые углы здания;
• абсолютное соблюдение размеров – не допустимы погрешности;
• необходимо отдельно проводить разметку внутреннего и внешнего контура;
• отдельно измеряют глубину основания;

Разметка основания из бетонных блоков, проводится после этапа заливки фундамента смесью. Выполнять разметку в этом случае, следует только после высыхания бетонной смеси и демонтажа опалубки. Отмечается на рейках верхняя линия основания, от которой делается разметка с интервалом 20см. Требуется точно соблюдать технологию, так как малейшие неточности приведут к тому, что здание будет иметь перекосы, а это чревато его обрушением и дальнейшими сложностями в процессе эксплуатации.

Полезные материалы

Особенности монтажа свайного фундамента

Конструкция свайного фундамента представляет собой так называемое «свайное поле», которое состоит из свай.

 

Свайные работы, подготовка, погружение

Производство свайных работ – это целый комплекс мероприятий по погружению свай в грунт на проектную глубину.

 

Монолитные ленточные фундаменты

Ленточный монолитный фундамент имеет жёсткую конструкцию с неразрывной структурой, формирующей замкнутый контур.

 

 

Diagonal Formula – GeeksforGeeks

В геометрии формы и структуры глубоко анализируются для определения их свойств и других конкретных параметров, связанных с ними.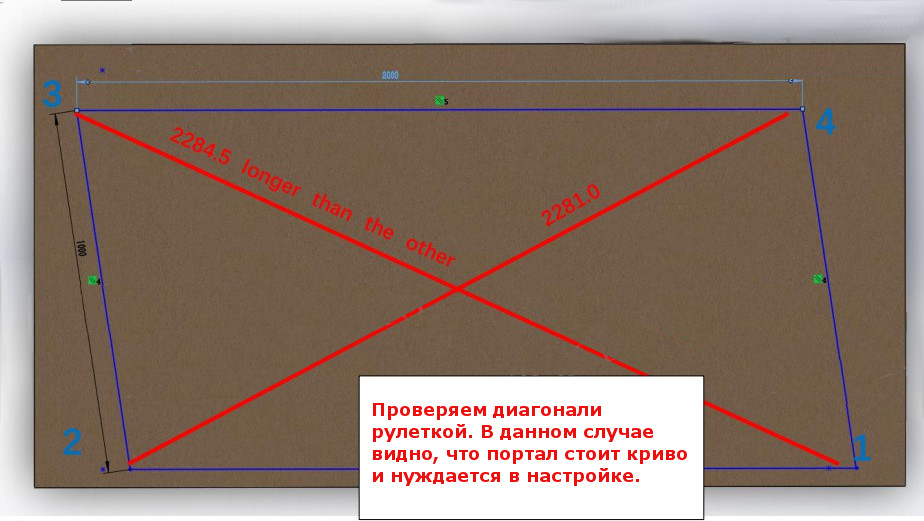 Поле включает в себя все формы формы для изучения и дает определенные формулы для расчета их параметров по мере необходимости.

Данная статья посвящена изучению диагоналей прямосторонних фигур. В содержание входит диагональная формула, которая помогает определить длину диагоналей данной конкретной фигуры.

Диагональ

Диагональ — это наклонный отрезок, соединяющий любые две вершины данного многоугольника, находящиеся на двух разных ребрах или сторонах. Это прямые или наклонные линии, соединяющие два противоположных угла квадрата, прямоугольника, ромба и других фигур.

Свойства диагоналей

• Диагонали многоугольника конгруэнтны.
• Каждая диагональ многоугольника делит другую пополам.
• Диагональ симметрично делит многоугольник.

Формула диагонали

Формула диагонали — это формула для диагонали, используемая для определения количества диагоналей в многоугольнике и длин диагоналей. Для расчета количества диагональных линий n-стороннего многоугольника дается выражение

n-стороннего многоугольника = n(n – 3)/2

Где

 n – количество сторон многоугольника.

 В геометрии существуют разные диагональные формулы для разных многоугольников, изучаемых в геометрии. Эти формулы специально используются для конкретного полигона. Приведены формулы этих многоугольников.

• Формула диагонали квадрата

Диагональ квадрата = a√2

, где

a – длина стороны квадрата.

• Формула диагонали прямоугольника

Диагональ прямоугольника =

Где

l — длина прямоугольника.

b — ширина прямоугольника.

• Диагональная формула ромба

Диагональ ромба = p = 2(A)/q

(Or)

q = 2(A)/p

Где

p и q — диагонали ромба

Площадь Rombus

• Диагональная формула параллелограммы

(OR)

также,

1111111111111111111111111111111111111111111111111111111111111111111111 211111111111111111111111111111111111111111111111111111111111111111111Р1н . (а ² + б ² )

Где,

x и y стороны параллелограмма

p и q две диагонали параллелограмма

Примеры задач меры 10 см.

Решение:

Дано,

Длина стороны 10см.

Диагональ квадрата = a√2

=> 10√2

=> 14,14см.

Вопрос 2: Найдите длину диагоналей квадрата со стороной 12 см.

Решение:

Дано,

Длина стороны 12см.

Диагональ квадрата = a√2

= 12√2

= 16,97см

Решение:

Дано,

Пусть две диагонали равны p и q.

Длина диагонали p 20см.

Площадь ромба 200 см

Вопрос 4: Найдите первую диагональ ромба, вторая диагональ которого равна 5 см, а площадь ромба равна 100 см ² .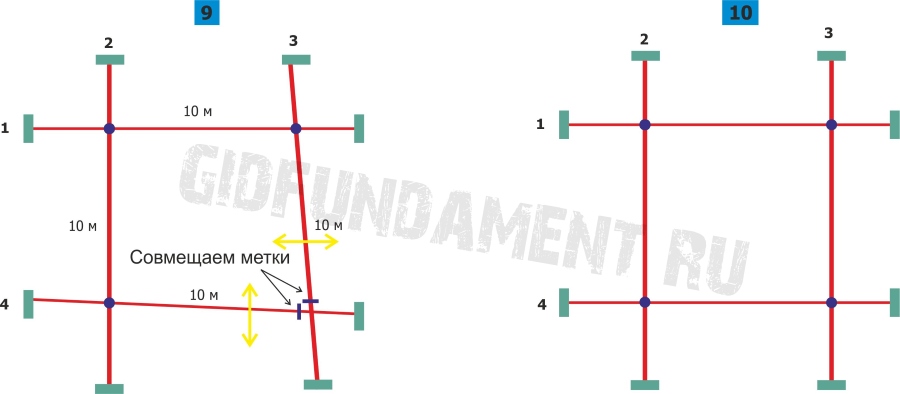

Решение:

Дано,

Пусть две диагонали равны p и q.

Длина диагонали q равна 5см.

Площадь ромба 100 см ²

p = 2(A)/q

=> p = 2 × 100/5

=> p = 200/5

см

=> 9 = 403

Вопрос 5: Найдите длину диагонали прямоугольника, длина которого 10 см, а ширина 3 см.

Решение:

Дано,

Длина прямоугольника 10см.

Ширина прямоугольника 3см.

Мы имеем

Диагональ прямоугольника =

=> √ (10) ² +(3) ²

=> ^{√ (100 +9)}

=> √109

=> 10,4444. см

Вопрос 6: Найдите длину диагонали прямоугольника, длина которого 20см, а ширина 12см.

Решение:

Дано,

Длина прямоугольника 10см.

Ширина прямоугольника 3см.

Мы имеем

Диагональ прямоугольника =

=> √ (20) ² + (12) ²

=> √ (400 + 144)

=> √544

=> 23,32C.

Как найти длину диагонали ромба?

Ромб также известен как четырехугольник с четырьмя сторонами. Считается частным случаем параллелограмма. Ромб имеет параллельные противоположные стороны и равные противоположные углы. Ромб также известен под названием алмаз или ромбовидный алмаз. У ромба все стороны ромба равны по длине. Кроме того, диагонали ромба пересекаются пополам под прямым углом.

Свойства ромба

Ромб обладает следующими свойствами: 

• У ромба все стороны равны.
• Диагонали ромба делят друг друга пополам под прямым углом.
• Противоположные стороны ромба по своей природе параллельны.
• Сумма двух смежных углов ромба равна 180 ^o .
• В ромбе нет вписанной окружности.
• Вокруг ромба нет описанной окружности.
• Диагонали ромба образуют четыре прямоугольных треугольника.
• Эти треугольники конгруэнтны друг другу.
• Противоположные углы ромба равны.
• При соединении середины сторон ромба образуется прямоугольник.
• При соединении середины половины диагонали образуется еще один ромб.

Диагональ ромба

Четыре ребра ромба соединены вершинами. При соединении противоположных вершин ромба образуются дополнительные ребра, в результате чего образуются диагонали ромба. Следовательно, ромб может иметь две диагонали, каждая из которых пересекается под углом 90°.

Свойства диагоналей ромба

Диагонали ромба обладают следующими свойствами:

• Диагонали делят друг друга пополам под прямым углом.
• Диагонали ромба делятся на четыре равных прямоугольных треугольника.
• Диагонали ромба могут быть или не быть равными по длине.

Вычисление диагонали ромба 

Длину диагоналей ромба можно вычислить следующими методами: 

По теореме Пифагора

Примем d ₁ за диагональ ромба.

Поскольку, как мы знаем, все смежные стороны ромба образуют угол 90 градусов.

Следовательно,

В треугольнике BCD имеем

BC ² + CD ² = BD ²

Теперь имеем, , 

Квадрат Диагональ: a√2

, где a – длина стороны квадрата

В случае прямоугольного ромба, мы имеем

Прямоугольник Диагональный: √ [L ² + B ² ]

где

• l — длина прямоугольника.
• b — ширина прямоугольника.

Используя площадь ромба

Рассмотрим O как точку пересечения двух диагоналей, а именно d ₁ и д ₂ .

Теперь, 

Площадь ромба эквивалентна, 

A = 4 × площадь ∆AOB

= 4 × (½) × AO × OB кв. единиц

= 4 × (½) × ( ½) d ₁ × (½) d ₂ кв. шт.

= 4 × (1/8) d ₁ × d ₂ кв.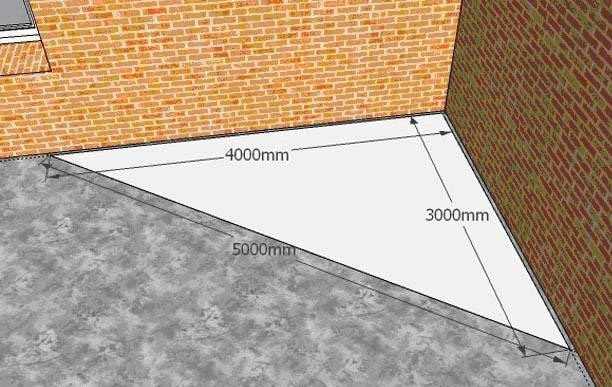 шт. 2

Следовательно, Площадь ромба = A = ½ × d ₁ × d ₂

Площадь ромба по диагоналям

Рассмотрим ромб ABCD, имеющий две диагонали, т. е. AC и BD.

• Шаг 1: Вычислите длину отрезка AC, соединив точки A и C. Пусть это будет диагональ 1, т.е. d ₁ .

Диагонали ромба перпендикулярны друг другу и стягивают прямоугольные треугольники при пересечении друг с другом в центре ромба.

• Шаг 2: Аналогичным образом вычислите длину диагонали 2, т. е. d ₂ , которая является расстоянием между точками B и D. и д ₂ .
• Шаг 4: Результат получается делением произведения на 2.

Результат даст площадь ромба ABCD.

Примеры вопросов

Вопрос 1. Одна из сторон ромба равна 5 см. Одна из диагоналей ромба равна 8 см, вычислите длину другой диагонали.

Решение:

Предположим, что ABCD — ромб, где AC и BD — диагонали.

Имеем, 

Сторона ромба равна 5 см  

BD = 8 см   

Так как, мы знаем, что диагонали ромба перпендикулярно делят друг друга пополам.

∴ BO = 4см

По теореме Пифагора имеем,

 В прямоугольном △AOB,  

⇒  (AB) ² = (AO) ^{2 (901 BO)0111 2}            

⇒  (5) ² = (AO) ² + (4) ²  

⇒  25 = (AO) ² + 16  

⇒  (AO) ² = 9

∴  AO = 3 см  

⇒  AC = 2 × 3 = 6 см  

∴  Длина другой диагонали ромба эквивалентна 6 см.

Вопрос 2. Вычислите площадь ромба, диагонали которого равны 6 см и 8 см соответственно.

Решение:

We know,

Diagonal 1, d ₁ = 6 cm

Diagonal 2, d ₂ = 8 cm

Area of ​​a rhombus, A = (d ₁ × d ₂ ) / 2

Подставляя значения,

= (6 × 8) / 2

= 48 / 2

= 24 см

2

Следовательно, площадь ромба равна 11 2 909 см 2 .