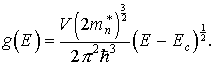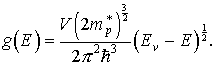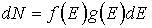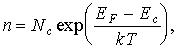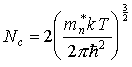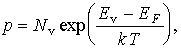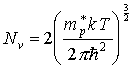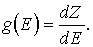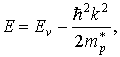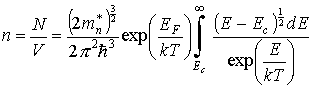- 3. Функция плотности состояний электронов и дырок
- 3. Функция плотности состояний электронов и дырок
- Физические процессы в p-n переходах. Физический смысл понятия “Эффективная плотность состояний”
- 5.4. Плотность состояний для электронов и дырок в полупроводниках.
- эффективная плотность состояний (на 1 см3) в зоне проводимости).
- Состояний плотность в зоне проводимости
- 3. Статистика электронов и дырок. Функции распределения. Плотность квантовых состояний в зоне.
3. Функция плотности состояний электронов и дырок
Для определения числа частиц, имеющих
энергию в заданном интервале, необходимо,
кроме функции распределения  ,
знать функцию плотности состояний
,
знать функцию плотности состояний .
Эта функция описывает распределение
уровней в соответствующих зонах и
определяет число уровней, приходящихся
на единичный интервал энергии. По
определению
.
Эта функция описывает распределение
уровней в соответствующих зонах и
определяет число уровней, приходящихся
на единичный интервал энергии. По
определению
| (8) |
Здесь, как и раньше, dZ– число возможных состояний ансамбля частиц (число уровней) с энергией, заключенной в интервале от
| (9) |
здесь 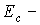 энергия
дна зоны проводимости,
энергия
дна зоны проводимости, –
эффективная масса электрона у дна зоны
проводимости,k– квазиимпульс
электрона,
–
эффективная масса электрона у дна зоны
проводимости,k– квазиимпульс
электрона, –
его компоненты. Согласно граничным
условиям, компоненты квазиимпульса
могут принимать только следующие
дискретные значения энергии:
–
его компоненты. Согласно граничным
условиям, компоненты квазиимпульса
могут принимать только следующие
дискретные значения энергии:

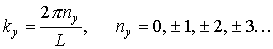

Каждому набору чисел nx,ny,nzотвечает
некоторое квантовое состояние (квантовый
уровень). В пространстве волновых
векторов каждому квантовому состоянию
соответствует объем ,
гдеV– объем кристалла. Эти элементарные
кубические ячейки займут в пространстве
волновых чисел объем шара радиусом
,
гдеV– объем кристалла. Эти элементарные
кубические ячейки займут в пространстве
волновых чисел объем шара радиусом
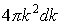 .
Разделив этот объем на объем элементарной
ячейки и умножив на 2, поскольку в каждом
состоянии могут находиться по два
электрона с противоположно направленными
спинами, получим число состояний в
объеме шарового слоя:
.
Разделив этот объем на объем элементарной
ячейки и умножив на 2, поскольку в каждом
состоянии могут находиться по два
электрона с противоположно направленными
спинами, получим число состояний в
объеме шарового слоя: | (10) |
Согласно (9)


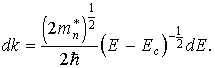
Подставляя значения k2 иdkв формулу (10), получим
 .
.
Учитывая (8), получим окончательное выражение для плотности квантовых состояний электронов у дна зоны проводимости:
| (11) |
Энергию дырок у потолка валентной зоны можно записать также в виде параболического закона:
| (12) |
где Ev– энергия потолка
валентной зоны,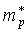 –
эффективная масса дырки. Вычисления,
аналогичные тем, которые были проведены
выше для электронов, приводят к следующему
выражению для функции плотности состояний
дырок вблизи потолка валентной зоны:
–
эффективная масса дырки. Вычисления,
аналогичные тем, которые были проведены
выше для электронов, приводят к следующему
выражению для функции плотности состояний
дырок вблизи потолка валентной зоны:
| (13) |
Следует подчеркнуть, что формулы (11) и (13) справедливы только для состояний вблизи экстремумов энергии, т.е. у дна или потолка энергетической зоны. В средней же части зоны точный вид функции
g(E) неизвестен. На рис. 4 схематически представлены зависимости плотности квантовых уровней вблизи дна зоны проводимости и потолка валентной зоны. 
Рис. 4. Плотность уровней в зоне проводимости и в валентной зоне
Площадь заштрихованных областей пропорциональна числу уровней dZв интервале энергийdE
4. Концентрации электронов и дырок в полупроводнике. Закон действующих масс. Невырожденный газ электронов и дырок
Вычислим концентрацию электронов в зоне проводимости полупроводника. Число электронов dN, находящихся вdZсостояниях энергетической зоны в соответствии с уравнением (1) определяется выражением

Учитывая, что dZ = g(E) dE, получим
| (14) |
Общее число электронов в зоне проводимости найдем, проинтегрировав выражение (14) в пределах зоны
| (15) |
здесь Еп– энергия потолка зоны проводимости. Поскольку функция распределения Ферми-Дирака очень быстро уменьшается с увеличением энергии, то верхний предел интегрирования можно взять равным бесконечности. Если степень заполнения энергетических состояний электронами в зоне проводимости мала (
f(E)<< 1), что практически всегда имеет место в полупроводниках, то единицей в знаменателе формулы (4) можно пренебречь. При этих условиях подстановка функцийf(E)иg(E)в уравнение (15) приводит к следующему выражению для концентрации электронов в зоне проводимости:
| (16) |
Преобразуем теперь выражение (16) к виду
 .
.
Произведем замену переменных в подынтегральном выражении

В результате получим
 .
.
Интеграл в этом выражении равен 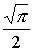 .
Следовательно
.
Следовательно
| (17) |
где
| (18) |
Величину Ncназывают
эффективной плотностью состояний в зоне проводимости. Аналогично можно вычислить концентрацию дырок в валентной зоне. Поскольку вакантное состояние в валентной зоне образуется в результате перехода электрона из этого состояния в зону проводимости, то вероятность того, что состояние с энергиейЕв валентной зоне не занято, равна .
.Тогда концентрация дырок

здесь Ev– потолок валентной зоны.
При условии, что газ дырок невырожденный, получим
|
где эффективная плотность состояний в валентной зоне
| (20) |
Перемножая выражения (17) и (19), получим
| (21) |
где ni– концентрация собственных носителей заряда в полупроводнике,Eg=Ec Ev– ширина запрещенной зоны.
Соотношение (21) называется законом действующих масс. При выводе этого закона использовано предположение о том, что степень заполнения энергетических уровней носителями заряда много меньше единицы. Такой газ носителей называетсяневырожденным, а полупроводники –невырожденными.
В общем случае вырожденным газом в физике называется газ, свойства которого отличаются от свойств идеального классического газа вследствие квантово – механических свойств частиц газа. Вырожденный газ подчиняется квантово – механическим статистикам Ферми-Дирака или Бозе -Эйнштейна, невырожденный газ – статистике Максвелла – Больцмана. Условием перехода газа в невырожденное состояние является выполнение неравенства f(E)<< 1. Можно показать, что это условие для электронного газа эквивалентно следующему соотношению:
| (22) |
Аналогичное соотношение справедливо
и для дырок с заменой nнаpи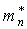 на
на .
.
Вопрос о том, является газ носителей заряда в кристалле вырожденным или невырожденным определяется только его концентрацией и температурой. Подстановка численных значений величин, входящих в неравенство (22), приводит к выводу о том, что при комнатной температуре (Т~ 300К) газ носителей будет невырожденным, если его концентрация значительно меньше 1025м-3(1019см-3). Это условие выполняется практически для всех полупроводников. Поскольку концентрация электронов в зоне проводимости металлов превышает 1028м-3(1022см-3), то электронный газ металлов всегда является вырожденным.
Таким образом, закон действующих масс
выполняется для любого невырожденного
полупроводника независимо от роли
примесей, т.е. в любом невырожденном
полупроводнике увеличение концентрации
носителей одного знака приводит к
уменьшению концентрации носителей
противоположного знака. Следует отметить
также, что произведе ние
электронной и дырочной концентраций
не зависит от положения уровня Ферми.
ние
электронной и дырочной концентраций
не зависит от положения уровня Ферми.
studfile.net
3. Функция плотности состояний электронов и дырок
Для определения числа частиц, имеющих
энергию в заданном интервале, необходимо,
кроме функции распределения  ,
знать функцию плотности состояний
,
знать функцию плотности состояний .
Эта функция описывает распределение
уровней в соответствующих зонах и
определяет число уровней, приходящихся
на единичный интервал энергии. По
определению
.
Эта функция описывает распределение
уровней в соответствующих зонах и
определяет число уровней, приходящихся
на единичный интервал энергии. По
определению
| (8) |
Здесь, как и раньше, dZ– число возможных состояний ансамбля частиц (число уровней) с энергией, заключенной в интервале отEдоE+dE. Функциюg(E)вычислим для кубического кристалла со сторонойL. Энергия электрона у дна зоны проводимости(Е(к) дать рисунок) приближенно может быть представлена в виде
| (9) |
здесь 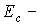 энергия
дна зоны проводимости,
энергия
дна зоны проводимости, –
эффективная масса электрона у дна зоны
проводимости,k– квазиимпульс
электрона,
–
эффективная масса электрона у дна зоны
проводимости,k– квазиимпульс
электрона, –
его компоненты. Согласно граничным
условиям, компоненты квазиимпульса
могут принимать только следующие
дискретные значения энергии:
–
его компоненты. Согласно граничным
условиям, компоненты квазиимпульса
могут принимать только следующие
дискретные значения энергии:



Каждому набору чисел nx,ny,nzотвечает
некоторое квантовое состояние (квантовый
уровень). В пространстве волновых
векторов каждому квантовому состоянию
соответствует объем ,
гдеV– объем кристалла. Эти элементарные
кубические ячейки займут в пространстве
волновых чисел объем шара радиусомk,
соответствующего максимально возможному
значению модуля волнового вектора.
Выделим шаровой слой, заключенный между
двумя поверхностямиk=constиk+dk =const. Объем этого слоя составляет
,
гдеV– объем кристалла. Эти элементарные
кубические ячейки займут в пространстве
волновых чисел объем шара радиусомk,
соответствующего максимально возможному
значению модуля волнового вектора.
Выделим шаровой слой, заключенный между
двумя поверхностямиk=constиk+dk =const. Объем этого слоя составляет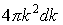 .
Разделив этот объем на объем элементарной
ячейки и умножив на 2, поскольку в каждом
состоянии могут находиться по два
электрона с противоположно направленными
спинами, получим число состояний в
объеме шарового слоя:
.
Разделив этот объем на объем элементарной
ячейки и умножив на 2, поскольку в каждом
состоянии могут находиться по два
электрона с противоположно направленными
спинами, получим число состояний в
объеме шарового слоя:
| (10) |
Согласно (9)
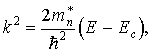
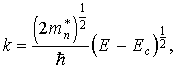
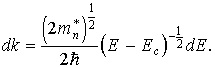
Подставляя значения k2 иdkв формулу (10), получим
 .
.
Учитывая (8), получим окончательное выражение для плотности квантовых состояний электронов у дна зоны проводимости:
| (11) |
Энергию дырок у потолка валентной зоны можно записать также в виде параболического закона:
| (12) |
где Ev– энергия потолка
валентной зоны,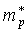 –
эффективная масса дырки. Вычисления,
аналогичные тем, которые были проведены
выше для электронов, приводят к следующему
выражению для функции плотности состояний
дырок вблизи потолка валентной зоны:
–
эффективная масса дырки. Вычисления,
аналогичные тем, которые были проведены
выше для электронов, приводят к следующему
выражению для функции плотности состояний
дырок вблизи потолка валентной зоны:
| (13) |
Следует подчеркнуть, что формулы (11) и (13) справедливы только для состояний вблизи экстремумов энергии, т.е. у дна или потолка энергетической зоны. В средней же части зоны точный вид функции g(E) неизвестен. На рис. 4 схематически представлены зависимости плотности квантовых уровней вблизи дна зоны проводимости и потолка валентной зоны.
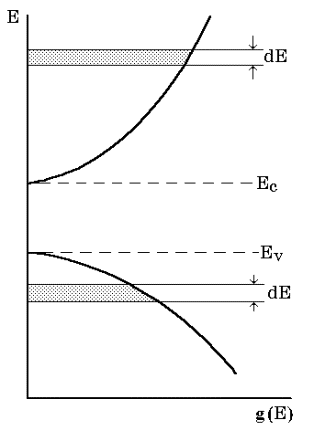
Рис. 4. Плотность уровней в зоне проводимости и в валентной зоне
Площадь заштрихованных областей пропорциональна числу уровней dZв интервале энергийdE
4. Концентрации электронов и дырок в полупроводнике. Закон действующих масс. Невырожденный газ электронов и дырок
Вычислим концентрацию электронов в зоне проводимости полупроводника. Число электронов dN, находящихся вdZсостояниях энергетической зоны в соответствии с уравнением (1) определяется выражением
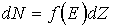 .
.
Учитывая, что dZ = g(E) dE, получим
| (14) |
Общее число электронов в зоне проводимости найдем, проинтегрировав выражение (14) в пределах зоны
| (15) |
здесь Еп– энергия потолка зоны проводимости. Поскольку функция распределения Ферми-Дирака очень быстро уменьшается с увеличением энергии, то верхний предел интегрирования можно взять равным бесконечности. Если степень заполнения энергетических состояний электронами в зоне проводимости мала (f(E)<< 1), что практически всегда имеет место в полупроводниках, то единицей в знаменателе формулы (4) можно пренебречь. При этих условиях подстановка функцийf(E)иg(E)в уравнение (15) приводит к следующему выражению для концентрации электронов в зоне проводимости:
| (16) |
Преобразуем теперь выражение (16) к виду
 .
.
Произведем замену переменных в подынтегральном выражении

В результате получим
 .
.
Интеграл в этом выражении равен  .
Следовательно
.
Следовательно
| (17) |
где
| (18) |
Величину Ncназываютэффективной плотностью состояний в
зоне проводимости. Аналогично можно
вычислить концентрацию дырок в валентной
зоне. Поскольку вакантное состояние в
валентной зоне образуется в результате
перехода электрона из этого состояния
в зону проводимости, то вероятность
того, что состояние с энергиейЕв
валентной зоне не занято, равна .
.
Тогда концентрация дырок
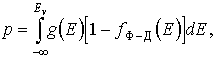
здесь Ev– потолок валентной зоны.
При условии, что газ дырок невырожденный, получим
| (19) |
где эффективная плотность состояний в валентной зоне
| (20) |
Перемножая выражения (17) и (19), получим
| (21) |
где ni– концентрация собственных носителей заряда в полупроводнике,Eg=Ec Ev– ширина запрещенной зоны.
Соотношение (21) называется законом действующих масс. При выводе этого закона использовано предположение о том, что степень заполнения энергетических уровней носителями заряда много меньше единицы. Такой газ носителей называетсяневырожденным, а полупроводники –невырожденными.
В общем случае вырожденным газом в физике называется газ, свойства которого отличаются от свойств идеального классического газа вследствие квантово – механических свойств частиц газа. Вырожденный газ подчиняется квантово – механическим статистикам Ферми-Дирака или Бозе -Эйнштейна, невырожденный газ – статистике Максвелла – Больцмана. Условием перехода газа в невырожденное состояние является выполнение неравенства f(E)<< 1. Можно показать, что это условие для электронного газа эквивалентно следующему соотношению:
| (22) |
Аналогичное соотношение справедливо
и для дырок с заменой nнаpи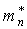 на
на .
.
Вопрос о том, является газ носителей заряда в кристалле вырожденным или невырожденным определяется только его концентрацией и температурой. Подстановка численных значений величин, входящих в неравенство (22), приводит к выводу о том, что при комнатной температуре (Т~ 300К) газ носителей будет невырожденным, если его концентрация значительно меньше 1025м-3(1019см-3). Это условие выполняется практически для всех полупроводников. Поскольку концентрация электронов в зоне проводимости металлов превышает 1028м-3(1022см-3), то электронный газ металлов всегда является вырожденным.
Таким образом, закон действующих масс
выполняется для любого невырожденного
полупроводника независимо от роли
примесей, т.е. в любом невырожденном
полупроводнике увеличение концентрации
носителей одного знака приводит к
уменьшению концентрации носителей
противоположного знака. Следует отметить
также, что произведе ние
электронной и дырочной концентраций
не зависит от положения уровня Ферми.
ние
электронной и дырочной концентраций
не зависит от положения уровня Ферми.
studfile.net
Физические процессы в p-n переходах. Физический смысл понятия “Эффективная плотность состояний”
Министерство образования РФ
ВлГУ
Кафедра КТРЭС
Лабораторная работа№1
Физические процессы в p-n переходах
Выполнил:
студент гр. РЭ-100
Проверил:
Владимир, 2002
1. Вопрос №7
Физический смысл понятия “Эффективная плотность состояний”
Физический смысл понятия “Эффективная плотность состояний” определяется в зоне проводимости и в валентной зоне. В зоне проводимости эффективная плотность состояний определяется формулой:


где NC – эффективная плотность состояний в зоне проводимости;
mn – эффективная масса электрона;
q – элементарный заряд;
φt– температурный потенциал;
h – постоянная Планка;
m – масса свободного электрона;
T – термодинамическая температура.
Из формулы (1) следует, что эффективная плотность состояний в зоне проводимости представляет собой максимально возможную концентрацию электронов в невырожденном полупроводнике. Понятие “эффективная плотность состояний” применимо в тех случаях, когда выполняется условие: энергия уровня Ферми стремиться быть равной энергии дна зоны проводимости. По физическому смыслу величина NCблизка к плотности энергитических уровней в зоне проводимости в полосе энергий от φс до φс+φt (где φс – энергия дна зоны проводимости, φt – температурный потенциал).
В валентной зоне эффективная плотность состояний определяется формулой:
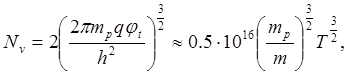
где NV – эффективная плотность состояний в валентной зоне;
mp – эффективная масса “дырки”;
q – элементарный заряд;
φt– температурный потенциал;
h – постоянная Планка;
m – масса свободного электрона;
T – термодинамическая температура.
Из формулы (2) следует, что эффективная плотность состояний в валентной зоне представляет собой максимально возможную концентрацию “дырок” в невырожденном полупроводнике. Понятие “эффективная плотность состояний” применимо в тех случаях, когда выполняется условие: энергия уровня Ферми стремиться быть равной энергии потолка валентной зоны. По физическому смыслу величина NVблизка к плотности энергитических уровней в валентной зоне в полосе энергий от φv до φv-φt (где φv – энергия потолка валентной зоны, φt – температурный потенциал).
2. Задача № 7
Условие:
Используя распределение Ферми-Дирака для примесного полупроводника

где Ndn – концентрация нейтральных атомов донорной примеси; Ed– энергия донорного уровня, определить относительную долю ионизированных атомов фосфора с энергией активации Ec-Ed=0.044 эВ при температурах 50, 100, 300 К.
Решение:
Относительная доля ионизированных атомов фосфора определяется распределением Ферми-Дирака:

где Ndn– концентрация нейтральных атомов донорной примеси;
Nd– концентрация ионизированных атомов донорной примеси;
Ec-Ed – энергиея активации;
k – коэффициент Больцмана;
T – термодинамическая температура.
При температуре, равной 300 К, уровень Ферми размещается в середине примесной зоны, поэтому разность между энергией донорного уровня и энергией уровня Ферми равна половине энергии активации:

Относительная доля ионизированных атомов фосфора при температуре – 300 К, равна:
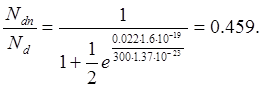
При более низких температурах (T=50 К; T=100 К) уровень Ферми располагается несколько ближе к дну зоны проводимости и дальше от донорного уровня, т.к. энергия электронов прямо пропорциональна kT, и им необходимо затратить большую энергию для достижения энергии уровня Ферми. Разность между энергией донорного уровня и энергией уровня Ферми изменяется не значительно, поэтому берётся такое же значение энергии активации как при температуре 300 К для 100 К:
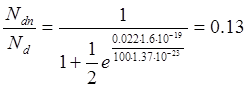 , для 50 К:
, для 50 К:

Ответ: для значений температур T=300 К, T=100 К и T=50 К полученны соответственно следующие результаты относительной доли ионизированных атомов фосфора: 0.459, 0.13, 0.1.
vunivere.ru
5.4. Плотность состояний для электронов и дырок в полупроводниках.
При анализе работы различных приборов
одной из важнейших характеристик
является число электронов dnв некотором интервале энергий, например
в интервалеdE. Для того, чтобы
определить это число, необходимо знать
число энергетических состояний в этом
интервале энергийdZи вероятность
заполнения этих состояний электронами,
или функцию распределения электронов
по энергиям .
.
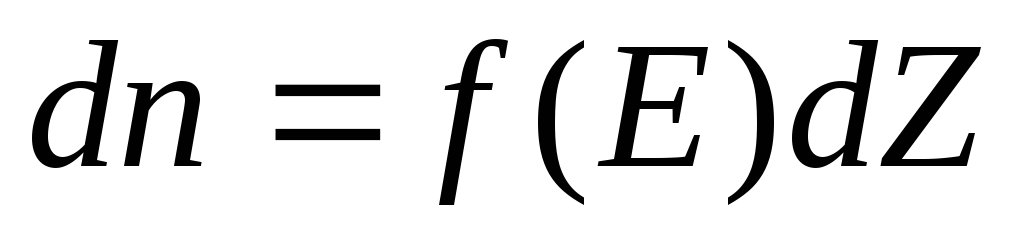 (5.13)
(5.13)
Число состояний можно получить через плотность энергетических состояний N(E), которую определим как число состояний в единичном интервале энергий в единице объёма полупроводника
 (5.14).
(5.14).
С учётом (5.14) выражение (5.13) запишется как
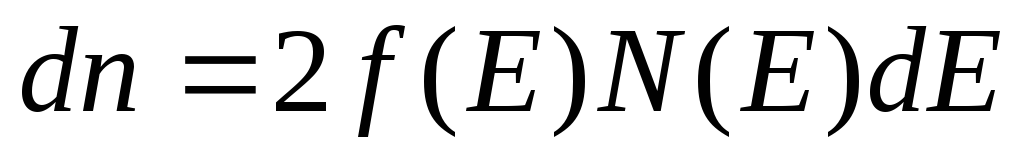 (5.15).
(5.15).
Множитель 2 в (5.15) отражает
принцип Паули, в соответствии с которым
в каждом квантовом состоянии может
находиться 2 электрона с противоположно
направленными спинами. Величина  определяется
формой изоэнергетических поверхностей
в пространстве квазиимпульсов. Положим,
пусть изоэнергетические поверхности
будут сферы – помним, что это соответствует
ситуации сферически симметричного
обратного пространства, поскольку
определяется
формой изоэнергетических поверхностей
в пространстве квазиимпульсов. Положим,
пусть изоэнергетические поверхности
будут сферы – помним, что это соответствует
ситуации сферически симметричного
обратного пространства, поскольку .
Тогда интервалу значенийdEв
пространстве квазиимпульсов будет
соответствовать объём шарового слоя
между изоэнергетическими поверхностями
с радиусамириp+dp. Этот объём
будет равен4p2dp.
Этому объёму пусть соответствует
реальный объёмV. Тогда объём в
фазовом пространствеdГ, соответствующий
интервалу значений энергииdEбудет
.
Тогда интервалу значенийdEв
пространстве квазиимпульсов будет
соответствовать объём шарового слоя
между изоэнергетическими поверхностями
с радиусамириp+dp. Этот объём
будет равен4p2dp.
Этому объёму пусть соответствует
реальный объёмV. Тогда объём в
фазовом пространствеdГ, соответствующий
интервалу значений энергииdEбудет
dГ =V4p2dp(5.16).
В этом объёме будет dZ квантових состояний, которое определяется как
 (5.17),
(5.17),
а на единицу объёма таких состояний будет
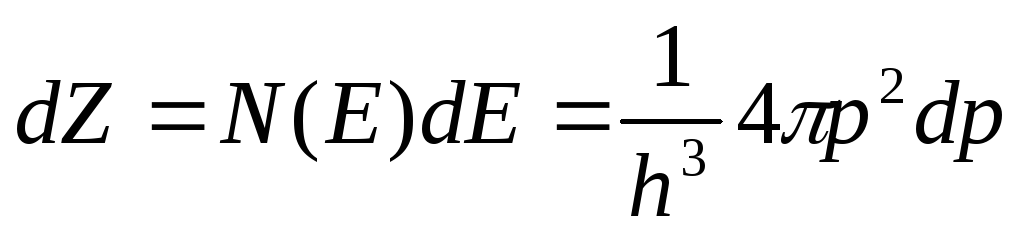 (5.18).
(5.18).
Начало отсчёта энергии совместим с минимумом энергии в зоне проводимости. Тогда, в соответствии с (4.15)
 (5.19).
(5.19).
Подставляем выражения (5.19) в (5.18) и получим
 (5.20),
(5.20),
откуда следует, что
 (5.21)
(5.21)
Аналогичное выражение может быть получено для плотности состояний вблизи потолка валентной зоны.
Лекция 6.
6.1. Функция распределения. Вырожденные и невырожденные полупроводники.
Мы определили плотность состояний как число состояний в единичном интервале энергий в единице объёма. Тогда концентрация электронов будет определяться как
 (6.1)
(6.1)
Здесь пределами интегрирования являются минимальная и максимальная энергии электронов в первой зоне Бриллюэна зоны проводимости. Если начало отсчёта энергии совместить с минимумом энергии в зоне проводимости, то нижний предел в интеграле (6.1) будет равным нулю, а верхний предел можно положить равным бесконечности, поскольку электроны занимают состояния вблизи дна зоны проводимости и функция распределения, как мы увидим ниже, резко спадает с увеличением энергии. В таком случае, вместо (6.1) получим
 (6.2).
(6.2).
Как мы помним из общего курса физики, электроны являются фермионами12, и для них необходимо использовать функцию распределения Ферми-Дирака
 (6.3)
(6.3)
З десьkT– тепловая энергия,F– энергия Ферми. На рис. 6.1 показана
зависимостьf(E)при разных температурах.
Из этого рисунка видно, что энергию
(уровень) Ферми можно определить двояко.
Во-первых, это есть максимальная энергия
электронов при0 Ки, во-вторых – это
есть уровень, вероятность заполнения
которого при всех температурах равна
½. Из (6.3) видно, что функция распределения
Ферми-Дирака, а следовательно, и
концентрация электронов в зоне
проводимости, зависят от температуры
и энергии.
десьkT– тепловая энергия,F– энергия Ферми. На рис. 6.1 показана
зависимостьf(E)при разных температурах.
Из этого рисунка видно, что энергию
(уровень) Ферми можно определить двояко.
Во-первых, это есть максимальная энергия
электронов при0 Ки, во-вторых – это
есть уровень, вероятность заполнения
которого при всех температурах равна
½. Из (6.3) видно, что функция распределения
Ферми-Дирака, а следовательно, и
концентрация электронов в зоне
проводимости, зависят от температуры
и энергии.
Для полупроводников различают два
крайних случая. 1. Если уровень Ферми
находится в запрещённой зоне, так что  ,
то в этом случае показатель степени в
(6.3) больше 1 и функция распределения
Ферми-Дирака переходит в классическую
функцию Максвелла-Больцмана
,
то в этом случае показатель степени в
(6.3) больше 1 и функция распределения
Ферми-Дирака переходит в классическую
функцию Максвелла-Больцмана
 (6.4).
(6.4).
Полупроводник при этом называется невырожденными концентрация электронов (6.2) с функцией распределения (6.3) при этом определяется выражением
 (6.5).
(6.5).
Здесь – так называемая эффективная
плотность состояний для зоны
проводимости.
– так называемая эффективная
плотность состояний для зоны
проводимости.
В противоположном случае, когда уровень
Ферми находится в зоне проводимости,
причём  ,
полупроводник называется вырожденным
и для нахождения концентрации необходимо
использовать функцию Ферми-Дирака
(6.3). При этом, с хорошей точностью
получается13
,
полупроводник называется вырожденным
и для нахождения концентрации необходимо
использовать функцию Ферми-Дирака
(6.3). При этом, с хорошей точностью
получается13
 (6.6)
(6.6)
Аналогичные выражения можно получить
и для дырочного полупроводника. На рис.
6.2 схематично показаны плотность
состояний Nc,
функция распределенияf(E)и произведение этих величин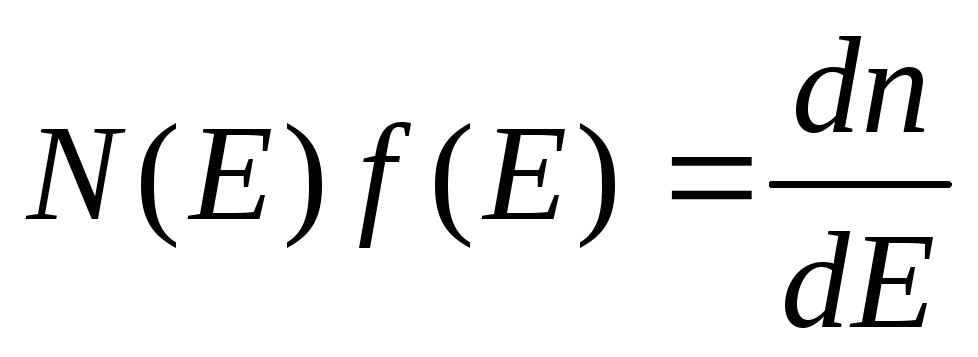 для невырожденного и вырожденного
полупроводников.
для невырожденного и вырожденного
полупроводников.
studfile.net
эффективная плотность состояний (на 1 см3) в зоне проводимости).
Электроника NС – эффективная плотность состояний (на 1 см3) в зоне проводимости).просмотров – 350
Величина Nд представляет собой концентрацию доноров. Из выражения видно, что уровень Ферми лежит ниже уровня дна зоны проводимости. Произведение концентраций электронов и дырок равно
.
Отсюда следует важный вывод о том, что произведение концентраций базовых и небазовых носителей заряда в примесном полупроводнике постоянно при заданной температуре и не зависит
от характера и количества содержащихся в нём примесей . Это соотношение часто используется в дальнейшем.
2.6.2. Полупроводник типа – p, или дырочного типа.
Введём теперь в германий примесь трёхвалентного индия.
В ковалентной связи будут участвовать только три валентных электрона индия, а связь с четвёртым соседним атомом германия будет неукомплектована (вакантна). Вакантное место может быть занято электроном из соседних атомов, где при этом образуется дырка.
Атом индия окажется ионизированным отрицательно. Изменяя концентрацию вводимых примесей, можно в широких пределах регулировать концентрацию дырок, образующихся при этом.
В таком полупроводнике концентрация дырок будет значительно преобладать над концентрацией электронов обусловленных термогенерацией пар электрон-дырка собственного полупроводника. Следовательно ток в таком примесном полупроводнике будет в основном обусловлен дырками. Примеси обусловливающие дырочную проводимость называются акцепторными, а сам полупроводник принято называть дырочным или
полупроводником p – типа. Энергетические уровни атомов акцепторов в p полупроводнике расположены вблизи потолка валентной зоны и при температуре отличной от нуля они полностью заняты электронами валентной зоны на энергетических уровнях которой образуются дырки.
Образовавшиеся дырки, концентрация которых на несколько порядков превышает концентрацию носителей заряда в собственном полупроводнике, обусловливают в основном дырочную проводимость такого полупроводника.
Как видно из рисунка, уровень Ферми p полупроводника смещён ближе к валентной зоне.
Концнетрация электронов и дырок в полупроводнике p-типа также рассчитывается на основании статистики Ферми- Дирака.
– для дырок,
-для электронов,
где WFp– уровень Ферми в полупроводнике p – типа.
(NV– эффективная плотность состояний в валентной зоне (на 1 см3вещества).
Величина Nапредставляет собой концентрацию акцепторов. Так же как и для n – полупроводника, для полупроводников типа p справедливо равенство .
Это равенство означает, что произведение концентраций электронов и дырок при данной температуре T для данного полупроводника постоянно и не зависит от характера и количества примесей.
В силу симметрии выражений, определяющих концентрацию базовых и небазовых носителей заряда в примесных полупроводниках, независимо от типа проводимости, их можно записать в следующем виде:
– для дырок, -для электронов,
где WF – уровень Ферми, определяемый для соответствующего типа полупроводника.
Поделив эти выражения друг на друга, приняв при этом n = ni2 / p и p = ni2 / n, можно привести
их к следующему виду: ,
где WFi = (Wc – Wv) / 2 – уровень Ферми в собственном полупроводнике, а WF – уровень Ферми в соттветствующем примесном полупроводнике.
Учитывая, что энергия электрона (дырки) W = q·φ, последние выражения для дырок и электронов соответственно можно привести к виду:
,.
где: φFi – потенциал Ферми в (вольтах) собственного полупроводника, φF – потенциал Ферми в (вольтах) соответствующего собственного полупроводника,
φT = k·T/q – температурный потенциал (в вольтах). При комнатной температуре
.
В некоторых учебниках, потенциал Ферми в собственном полупроводнике – φFi , заменяют потенциалом середины запрещённой зоны примесного полупроводника – φE, что практически одно и то же, т.к. φFi ≈ φE.
Тогда: ,
Из этих выражений непосредственно следует:
φFn = φE + φT · ln(n / n i ) – для полупроводников n – типа уровень Ферми смещён от середины запрещённой зоны вверх по диаграмме к свободной зоне на величину ln(n / n i ) и
φFp = φE – φT · ln(p / n i ) – для полупроводников p – типа уровень Ферми смещён от середины запрещённой зоны вниз по диаграмме к валентной зоне на величину ln(p / n i ) .
2.7. Электропроводность примесных полупроводников.
Так же как и для собственного полупроводника, проводимость примесного полупроводника, независимо от его типа : σ = q·n·μn + q·p·μp .
Принимая во внимание, что в электронном полупроводнике n>>p, σn ≈ q·n·μn , а в дырочном полупроводнике p>>n, σp ≈ q·n·μp, проводимость примесных полупроводников в основном определяется концентрацией базовых носителей заряда.
Пренебрегая в данном случае концентрацией небазовых носителей, будем остерегаться заблуждения относительно их роли в физических процессах, имеющих место в полупроводниковых приборах.
2.7.1. Зависимость электропроводности примесных полупроводников от температуры.
Зависимость проводимости σ от температуры определяется двумя факторами:
– зависимостью концентрации носителей заряда от температуры, а также зависимостью подвижности носителей заряда μnи μp от температуры. В области низких температур подвижность зарядов пропорциональна μ → T 3/2, а при высоких температурах μ→(1/T)3/2.
2.8. Электрический ток в примесном полупроводнике
Перемещение носителей заряда – электронов и дырок в полупроводнике вызывается двумя причинами.
1) Направленное перемещение под действием электрического поля, называемое дрейфом носителей заряда. Ток обусловленный дрейфом носителей заряда принято называть дрейфовым.
jn др = q·n·μn·E – для электронного тока, jp др = q·p·μp·E – для дырочного тока.
2) Направленное перемещение носителей заряда вследствие разности концентраций зарядов
(дырок или электронов) в смежных областях полупроводника. Ток, обусловленный
избыточностью заряда в некоторой ограниченной области полупроводника, принято называть диффузионным, а перемещение носителей заряда, стремящихся равномерно распределиться в объёме полупроводника, – диффузией.
jn диф. = q·Dn·grad n – для электронов, jp диф. = -q·Dp·grad p – для дырок.
Здесь Dn и Dp – коэффициенты диффузии электронов и дырок соответственно. Dn,p = φT·μn,p.
Полная плотность электронного и дырочного тока определяется суммой двух составляющих: – полный электронный ток
и – полный дырочный ток
Как правило, нас интересует движение носителей заряда в направлении одной из осей координат.
Обозначив это направление через x, для одномерной модели получим:
jn = jn др + jn диф = q·n·μn·E + q·Dn· д n/dx -для электронов, jp = jp др + jp диф = q·p·μp·E – q·Dp·д p/dx -для дырок.
Как электроны, так и дырки всегда движутся в направлении убывания концентрации носителей заряда, в связи с этим если выбранное положительное направление оси х совпадает с градиентом, то электронный ток будет иметь положительное направление, а дырочный ток отрицательное. Этим обясняется знак минус перед диффузионной составляющей дырочного тока в приведённых выше выражениях для плотностей токов.
3. КОНТАКТ ДВУХ ПОЛУПРОВОДНИКОВ РАЗЛИЧНОГО ТИПА ПРОВОДИМОСТИ.
3.1.Электронно – дырочный переход.
Под идеальным контактом двух полупроводников принято понимать такое их соединение, при котором:
1) – граница их раздела является абсолютно плоской.
2) – граница раздела не содержит вкраплений других элементов и дефектов кристаллической решётки, ᴛ.ᴇ. кристаллическая решётка одного полупроводника непрерывно переходит в кристаллическую решётку другого.
Так как основные носители заряда по обе стороны границы раздела имеют различные знаки, с одной стороны границы раздела возникает градиент концентрации дырок, а с другой электронов. Следовательно возникнет диффузия электронов из n полупроводника в p полупроводник и диффузия дырок из p области в n область, ᴛ.ᴇ. через границу раздела потечёт диффузионный ток.
Уход базовых носителей заряда, в первую очередь из близлежащих к границе раздела областей полупроводников, “оголяет” ионы атомов доноров и акцепторов, положительные в n и отрицательные в p полупроводнике, заряд которых ранее компенсировался основными носителями. Нескомпенсированные объёмные заряды по обе стороны границы раздела полупроводников создают электрическое поле напряжённостью E. Это поле препятствует дальнейшей диффузии базовых зарядов, но создаёт возможность дрейфа небазовых носителей заряда – дырок из n области в p область и электронов из p области в n область.
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, через границу раздела полупроводников текут две составляющие диф-фузионного тока базовых носителей заряда, направленные из p области в n область, а также две составляющие дрейфового тока небазовых носителей заряда, направленные из n области в p область. При этом “оголяются” всё более удалённые по обе стороны от границы раздела ионы, ᴛ.ᴇ. их объёмный заряд растёт.
Область объёмных зарядов на границе раздела полупроводников разного типа проводимости, обеднённая основными носителями заряда, принято называтьp-n переходом.
По мере увеличения объёмного заряда, а следовательно и напряжённости поля E, диффузионный ток уменьшается, а дрейфовый ток возрастает. Этот процесс продолжается до тех пор, пока лишь незначительная часть базовых носителей заряда, имеющих энергию, достаточно большую, для преодоления тормозящего действия поля, сможет перемещаться(прорываться) через границу раздела.
Когда диффузионный ток таких носителей заряда уравновесится, растущим по мере увеличения объёмного заряда, током небазовых носителей заряда, наступает состояние динамического равновесия. В этом состоянии токи в смежные области полупроводников уравновешивают друг друга, объёмный заряд перестаёт расти, суммарный ток через границу раздела равен нулю, т.к. внешняя цепь разомкнута.
Итак: jp др + jn др + jp диф + jnдиф = 0.
Читайте также
ПОСТАНОВЛЕНИЕ 117. Исполнитель ограничивает или приостанавливает предоставление коммунальной услуги, предварительно уведомив об этом потребителя, в случае: а) неполной оплаты потребителем коммунальной услуги – через 30 дней после письменного предупреждения… [читать подробенее]
… [читать подробенее]
… [читать подробенее]
Population density is the number of inhabitants per a unit of area. Population density depends on a number of factors: 1) natural conditions. Favorable climate, fertile soil and sea attract population. 80 of every 100 inhabitants live in lowland, i.e. lower than 500 meters above the sea level; 2) historical factor; 3) demographic factor. High or low natality can influence population density of a territory. 4) social and economic factors.These include occupational structure of… [читать подробенее]
III. Атрезия трехстворчатого клапана А. Встречаемость: 2-5% больных с синими пороками сердца. Б. Анатомия. 1. Присутствуют четыре основные аномалии: 1) атрезин трехстворчатого клапана, 2) ДМПП, 3) гипоплазия ПЖ, 4) ДМЖП. Кровь обычно поступает в ПЖ через ДМЖП. 2. У 30% больных… [читать подробенее]
… [читать подробенее]
… [читать подробенее]
… [читать подробенее]
… [читать подробенее]
… [читать подробенее]
oplib.ru
Состояний плотность в зоне проводимости
Здесь N — эффективная плотность состояний в зоне проводимости, определяемая выражением (7.133) g — фактор спинового вырождения примесного уровня. Обсудим физический смысл величины g. Полное число примесных состояний в запрещенной зоне равно числу примесных атомов, т. е. равно A d в расчете на единичный объем кристалла, поскольку каждый атом может отдать [c.252]В отличие от кристаллического полупроводника, где при комнатной температуре электроны с мелких донорных уровней переходят в зону проводимости, здесь они перейдут, в основном, на локализованные состояния вблизи уровня Ферми. При высокой плотности состояний это приводит к незначительному смещению уровня Ферми из положения Ер в положение и электрические свойства полупроводника практически не изменятся. Новое положение уровня Ферми может быть найдено из условия [c.365]
Итак, в полупроводнике надо рассматривать два статистических коллектива газ электронов проводимости и газ дырок. Поскольку электрон проводимости и дырка рождаются одновременно (в паре друг с другом), плотности обоих газов одинаковы. В термодинамическом равновесии уровни Ферми обоих газов совпадают общий уровень проходит примерно посередине запрещенной зоны. Если принудительно перебрасывать электроны из валентной зоны в зону проводимости (например, облучая полупроводник светом), то можно при данной температуре увеличить плотность газа электронов проводимости и соответственно плотность дырочного газа при этом полупроводник переходит в неравновесное состояние, уровень Ферми электронов проводимости поднимается, приближаясь к зоне проводимости, а уровень Ферми дырок опускается к валентной зоне. В неравновесном полупроводнике можно создать вырожденные газы электронов проводимости и дырок, должным образом [c.144]
В идеальном полупроводнике, если все электроны находятся в наинизшем энергетическом состоянии, в зоне проводимости не должно быть электронов. Такое положение теоретически возможно лишь при абсолютном нуле. При обычных температурах в зоне проводимости всегда найдется некоторое количество электронов, заброшенных туда из валентной зоны путем термического возбуждения. Мгновенная плотность электрического тока ], связанного с движением какого-либо электрона, пропорциональна его скорости у. Плотность тока, связанного с движением одного электрона в объеме Й, может быть представлена в виде [c.88]
График распределения плотности состояний собственного кристаллического полупроводника показан на рис. 4, а. В зоне проводимости и в валентной зоне такого полупроводника плотность состояний велика, а в запрещенной зоне — равна нулю. В запрещенной зоне электронного (рис. 4, б) и дырочного (рис. 4, в) кристаллических полупроводников появляется пик (заштрихован), соответствующий донорным или акцепторным уровням [c.9]
Число электронов в зоне проводимости и дырок в валентной зоне обычно значительно меньше числа энергетических состояний, содержащихся в этих зонах. Поэтому средняя плотность заполнения энергетических состояний электронами и дырками Г соответствует неравенству [c.52]
Под этим режимом принято понимать такое состояние кристалла, непрерывно освещаемого записываемой интерференционной картиной, при котором амплитуда решетки электрического поля остается неизменной во времени dE (.ldt = 0). Из уравнения (4.12) следует, что в подобном состоянии глубина модуляции плотности электронов в зоне проводимости а должна совпадать с глубиной модуляции [c.52]
Вывести закон действующих масс для концентраций основных и неосновных носителей в полупроводнике, предполагая, что для носителей тока в зоне проводимости и в валентной зоне, так же как для классических свободных частиц, применима статистика Максвелла — Больцмана и что функция плотности состояний параболическая для обеих зон. Эффективные массы т% (для электронов) и т р (для дырок) считать известными и постоянными. [c.77]
Ф и е, 48. Предполагаемая форма кривых плотности состояний в зоне проводимости и в d-зоне переходного металла. [c.125]
Согласно зонной теории твердого тела, если имеется достаточное число электронов для заполнения всех разрешенных энергетических состояний одной или нескольких зон и последняя заполненная зона не соприкасается и не перекрывается со следующей зоной, то при абсолютном нуле совершенный кристалл такого вещества является изолятором. При этом отсутствует перекрытие кривых зависимости плотности состояний от энергии (см. фиг, 2). Энергетический разрыв между самыми высокими занятыми состояниями и самыми низкими незанятыми называется областью запрещенных значений энергии или запрещенной зоной. При этом уровень Ферми проходит посредине запрещенной зоны. Если ширина запрещенной зоны мала, то при повышении температуры электроны из занятой зоны будут переходить на незанятые энергетические состояния следующей зоны. В этом случае приложение разности потенциалов приведет к появлению проводимости, поскольку имеется достаточно большое число незанятых состояний, по которым эти электроны могут свободно двигаться. Такие вещества известны под названием собственных полупроводников. Если ширина запрещенной зоны достаточно велика, то тепловая энергия, необходимая для активации электронов в зону проводимости, может оказаться настолько высокой, что это вызовет смещение и миграцию атомов или даже пробой твердого тела. Такое положение характерно для некоторых изоляторов при обычнЫх температурах. Значение ширины запрещенной зоны для гомологических рядов веществ является мерой прочности связи между атомами в кристалле. [c.262]
Рассмотрим полупроводник, в котором естественные процессы, происходящие при определенной температуре, достаточны для того, чтобы поддерживать заданную объемную плотность го свободных электронов в зоне проводимости (эта зона может принять гораздо большее число электронов). Данное значение плотности п при тепловом равновесии возникает в результате конкуренции двух противоположных процессов 1) генерации (со скоростью g) электронов проводимости путем возбуждения их из заполненных состояний с низкими энергиями и 2) рекомбинации (со скоростью г) свободных электронов путем обратного перехода в любое вакантное состояние с низкой энергией. [c.404]
Пороговая энергия соответствует расстоянию от максимума валентной зоны до минимума зоны проводимости (запрещенная зона). Это та минимальная энергия, которая должна быть сообщена электрону для того, чтобы он мог перейти в зону проводимости. Структура выше пороговой энергии определяется переходами с уровней валентной зоны в более высокие уровни зоны проводимости. Их вклад в б2 сильно зависит от того, где в зоне Бриллюэна лежат начальные и конечные состояния, насколько там велика плотность состояний, и от того, являются ли переходы между уровнями разрешенными нли запрещенными симметрией решетки. [c.261]
Оценим величину которая называется эффективной плотностью состояний в зоне проводимости (не путать с плотностью электронных состояний) [c.28]
Предположим, что мы нашли основное состояние электронов в диэлектрике в приближении независимых электронов. Низшее возбужденное состояние диэлектрика будет, очевидно, отвечать переносу электрона с самого высокого уровня в наиболее высоко расположенной заполненной зоне (т. е. в валентной зоне) на самый нижний уровень наинизшей незаполненной зоны (зоны проводимости) ). Такое изменение распределения электронов не влияет на самосогласованный потенциал, в котором они движутся см. (17.7) или (17.15)]. Это объясняется тем, что блоховские электроны не локализованы ( (г) Р -периодическая функция), поэтому локальное изменение плотности заряда, обусловленное переходом одного электрона на другой уровень, имеет порядок МЫ (поскольку только им часть заряда электрона окажется в некоторой выбранной элементарной ячейке), т. е. пренебрежимо мало. Поэтому для возбужденной конфигурации не надо проводить нового расчета электронных энергетических уровней энергия первого возбужденного состояния будет превышать энергию основного состояния на величину — 1 где — минимальная энергия в зоне проводимости, а. — максимальная энергия в валентной зоне. [c.244]
Предполагая, что функции плотности состояний определяются выражениями (8.2.5) и (8.2.6), а распределения электронов в зоне проводимости и дырок в валентной зоне—распределением Больцмана [формулы (7,2.4) и (7.2.5)1, показать, что п (г) и р (е) достигают максимальных значений при энергии кТ 2) от края зоны. Доказать, что диапазон энергий, при которых п ( ) и р (е) превышают (1/ /2) от максимального значения, составляет 1,1 кТ. [c.237]
Здесь п — полная концентрация электронов Ап( с) — концентрация электронов в зоне проводимости. Из рис. 11.11 и выражения 11.15) следует, что примесную проводимость можно получить, если каким-либо способом удастся снизить плотность состояний в запрещенной зоне. Второй путь — ввести в полупроводник большое количество примесных атомов так, чтобы перекомпенсировать дефектные состояния. Все это, разумеется, возможно при условии, что примесные атомы образуют донорные (или акцепторные) уровни в запрещенной зоне. [c.365]
Иная ситуация имеет место в вырожденных полупроводниках. Слабое вырождение приводит к уменьшению коэффициентов поглощения на частотах, близких к краю собственного поглощения. Сильное же вырождение вообще сдвигает край поглощения в сторону более коротких волн. Этот эффект называют сдвигом Бурштейна. Он отчетливо проявляется в полупроводниках с малой плотностью состояний у дна зоны проводимости (или у потолка валентной зоны), в которых сильное вырождение достигается при сравнительно малых уровнях легирования. Так, в InSb легирование донорами (концентрация 5 10 м ) приводит к сдвигу длинноволновой границы собственного поглощения с 7,1 до 3,5 мкм. Во многих же случаях сдвиг Бурштейна маскируется другим эффектом сильного легирования — изменением плотности состояний у краев энергетических зон. Это изменение происходит вследствие размытия примесных уровней в примесную зону и слияния последней с зоной проводимости или с валентной зоной. [c.322]
Переход П. т. т. в результате неустойчивости в состояние диссипативной пространственно-временной структуры может быть описан на языке неравновесного фазового перехода. Как правило, с изменением уровня возбуждения П. т. т. испытывает неск. неравновесных фазовых переходов, в результате к-рых одни диссипативные структуры заменяются другими. Примерами этих структур являются колебания концентрации носителей и (или) Т. Часто эти колебания сопровождаются изменением тока, проходящего через П. т. т. (в случае токовых неустойчивостей), так что П. т. т. в сочетании с внеш. электрич. цепью выступает как генератор электрич. колебаний. Др. примером служит инм-екционный лазер, где в результате инжекции электронов и дырок создаётся бинолярная плазма высокой плотности с инвертиров. заполнением электронных состояний в зоне проводимости по отношению к валентной зоне. Возникновение когерентного эл.-магн. излучения может быть описано как неравновесный фазовый переход. [c.604]Нестабильность валентности и возможность перехода /-электрона в зону проводимости и обратно (межконфи-гурац. флуктуации) существенно проявляются в большинстве физ. свойств систем с П, в, Т, к. энергия 4/-уровня лежит вблизи р, то размытие уровня приводит к появлению вблизи /р узкого пика в плотности состояний с шириной, пропорциональной V , где V — матричный элемент / — с-перехода (рис, 5), [c.142]
Н1э, — гл. компоненты тензора эффективной массы электрона и дырки, е — заряд электрона, Р — вектор поляризации света, е — матричные элементы операторов импульса электронов (дырок). Множитель (Йш—отражает зависимость плотностпи состояний в зоне проводимости (валентной зоне) от энергии кванта. Матричные элементы е слабо зависят от давления (как и постоянная решётки). Незначительно меняются и эфф. массы носителей, т. е, М. Осн, влияние давления связано со сдвигом электронных уровней, определяющих плотность состояний. Давление позволяет не только сдвигать электронные уровни, но и изменять электронный спектр. [c.188]
СОБСТВЕННАЯ ПРОВОДИМОСТЬ — проводимость полупроводника, обусловленная электронами, возбуждёнными из валентной зоны в зону нроводнмости я дырками, образовавшимися в валентной зоне. Крдцеятрацип п таких (зонных) электронов и дырок равны, и их можно, выразить через эфф, плотности состояний в зоне проводимости (Л д) и в валентной зоне (Nfi), ширину запрещённой зоны и абс. темп-ру Т [c.567]
Ландау впервые показал, что диамагнетизм электронов проводимости возникает в результате квантовомеханических эффектов. В магнитном поле диаметр орбиты квантуется. Легко показать [27], что плотность состояний не зависит от и имеет тот же вид, что и для свободных электронов (разд. 4. 2). Изменяется, однако, распределение состояний. Квазинепрерывный набор уровней в зоне проводимости превращается в набор дискретных квантовых уровней (фиг. 28). Каждый уровень отстоит от соседнего на энергию Н Ь.е1т с. Уровни между Ef и Ef — H Tielm ) сливаются в уровень Ef — и система оказывается [c.102]
Техника наблюдения была разработана Скиннером [39]. В первом приближении вероятность перехода электрона проводимости в связанное состояние пропорциональна плотности состояний. Поэтому форма рентгеновской L- (или М-) линии должна воспроизводить вид кривой, изображающей плотность состояний в зоне проводимости, а полная ширина линии должна давать энергетическую ширину зоны проводимости. На фиг. 39 показан вид кривой, полученной Скиннером для лития (или натрия). Как видно из графика, возникает трудность в определении того места, где исчезает хвост плотности состояний. Полученные таким путем значения ширины полосы заполненных состояний в зоне проводимости ( – – 0,4 эв) находятся в хорошем согласии со значениями, вычисленными на основе модели свободных электронов. [c.114]
В свободном атоме З -уровни сильно связаны (т. е. им соответствуют низкие энергии), поэтому, когда атомы сближаются и образуют кристалл, Зс -уровни будут уширяться меньше, чем 4s-ypoBHH (фиг. 47). Brf-зона пятикратно вырождена I = 2), и, поскольку ширина этой зоны AiE gd (фиг. 47) меньше, чем плотность состояний в Sd-зояе долж на быть гораздо больше, чем в зоне проводимости (фиг. 48). Если центр с -зоны расположен ненамного ниже верхнего края зоны проводимости и Зй-зона не заполнена (как это в действительности имеет место у переходных элементов), то можно ожидать, что уровень Ферми будет лежать в rf-зоне. Тогда плотность состояний на поверхности Ферми будет значительно больше, чем у нормальных металлов. Эти простые рассуждения качественно объясняют многие наблюдаемые свойства переходных металлов, зависяш.ие от плотности состояний, например их большую теплоемкость (разд. 6.2) и магнитную восприимчивость (разд. 6.3). [c.124]
Мы считаем, что в области I зона проводимости и валентная зона сильно перекрываются между собой. При очень высоких температурах (>1125°С) это не кажется неожиданным, поскольку при такой температуре запрещенная зона для ТЬТе, выведенная в гл. 7, 1, составляет примерно — 0,45 эВ. Однако в данном случае мы считаем, что плотность состояний в валентной зоне Nv) растет много быстрее, чем плотность состояний в зоне проводимости N ), возможно, вследствие Зс -состояний меди, так что при составе СигТе Ef) >N Ef), как показано на рис. 8.16. Это является причиной того, что S положительна. Большие температурные коэффициенты S и а объясняются [c.199]
В (2.40)(2.42) ыы уже перешли от описания распределения электронов по всей возможным энергетическим состояниям к описанию, в котором мы объединили группы электронов и группы незаполненных состояний в коллективы . Теперь, следовательно, нас интересует полное число электронов в зоне проводимости, дырок в валентной зопе, электронов в допорах и т. д. Концентрация частиц в таких коллективах может быть определена прп заданной зонной структуре (плотности состояний), температуре и концентрации дефектов. [c.90]
В полупроводниках при абсолютном нуле следует ожидать, что все состояния валентной зоны заняты, а все состояния зоны проводимости свободны. Поэтому можно сказать, что энергия Ферми лежит где-то внутри энергетической шели, разделяюшей обе разрешенные зоны. При конечной температуре вероятность заполнения не есть точно единица или точно нуль это означает, что некоторое малое число электронов оказывается возбужденным в зону проводимости, а в валентной зоне возникает небольшое число дырок. Для чистого (собственного) полупроводника оба числа должны быть равны, и это требование определяет энергию Ферми. В частности, если плотность состояний вблизи дна зоны проводимости такая же, как и вблизи края валентной зоны, то энергия Ферми должна лежать точно посередине шели между зонами. Если, с другой стороны, плотность состояний валентной зоны выше, тогда энергия Ферми должна лежать ближе к зоне проводимости. Обычно приходится определять энергию Ферми при тех температурах, которые нас интересуют, и в этом случае энергия Ферми сама оказывается зависящей от температуры (см. задачу 1 настоящей главы). [c.270]
Мелкие нримеси играют огромную роль в полупроводниках. Так как гпирпна запрегценной зоны ( обычно велика ( 1) по сравнению с кТ 300 К 0.025 эВ), термические забросы электронов из валентной зоны в зону проводимости из-за малой вероятности не приведут к заметной плотности свободных электронов и дырок. А энергии ионизации примесных атомов (4.10) сравнимы с/сТ, поэтому электроны или дырки связанных состояний могут с больпюй вероятностью переходить в непрерывный спектр (то есть в зону проводимости или валентную зону), определяя проводимость кристалла. [c.23]
Если же рассматривать электроны как вырожденный ферми-газ, то следует учитывать, что электроны заполняют все уровня в зоне проводимости вплоть до уровня Ферми хо = кТо (> кТ). Тепловая энергия, равная по порядку величины кТ, не может возбудить электронов с низколежащих уровней в силу принципа Паули. Поглотить энергию кТ и перейти на свободные уровни могут лишь электроны, находящиеся вблизи уровня Ферми. Это обусловлено тем, что в вырожденном случае функция распределения Ферми резко падает от 1 до О в области шириной порядка кТ вблизи уровня Ферми. Таким образом, число электронов, которые могут испытать тепловое возбуждение, имеет величину порядка МТ1То, так что вклад их в атомную теплоемкость имеет порядок ( /г) КТ Но, т. е. пренебрежимо мал при Г плотность состояний дается формулой (4.9). получаем для хр [c.287]
В (юлупроводниках энергетические уровни валентной зоны и зоны проводимости лежат так тесно, что их обычно рассматривают как непрерывное распределение. В 8.2 плотность энергетических уровней около энергии е,2 в зоне проводимости была выражена как 5с ( г)-Эквивалентная плотность уровней около энергии в валентной зоне (81). Типичный вид этих функций плотности состояний был приве- [c.272]
В 4 приводятся выражения для коэффициента поглощения и скоростей спонтанного и вынужденного излучений в полупроводниках. Эти выражения требуют вычисления матричного элемента и плотности состояний в зоне проводимости и валентной зоне. Для обычно встречающихся концентраций примеси в ак- тивных областях полупроводниковых лазеров плотность состояний в зоне проводимости н валентной зоие зависит от концентрации примеси,.что приводит к образованию хвостов зон внутри запрещенной зоны. Представление хвостов зон моделями Кейна [4] и Гальперина и Лэкса [5] дано в 5 этой главы. [c.133]
Рис. 3.4.1. а — зависимость плотности состояний в параболической зоне от энергии для = 0,07то п гпр = 0,5шо б —распределение дырок в валентной зоне н электронов в зоне проводимости для р = I 0 ° см и п = 1 см при Г = 297 К [c.151]
mash-xxl.info
3. Статистика электронов и дырок. Функции распределения. Плотность квантовых состояний в зоне.
Процессами, приводящими к образованию свободных электронов и дырок, являются:
1) переход электронов из валентной зоны в зону проводимости с образованием пары свободных носителей – электрона и дырки;
2) переход электрона с донорного уровня в зону проводимости с образованием свободного электрона и положительно заряженногоиона донорной примеси N+d;
3) переход электрона из валентной зоны на акцепторный уровень с образованием свободной дырки и отрицательно заряженного иона акцепторной примеси N–a .
Электроны, перешедшие в зону проводимости, занимают состояния с наименьшей энергией. Т.к. энергия дырок отсчитывается вниз, они занимают состояния с наименьшей энергией вблизи потолка валентной зоны.
Для нахождения равновесных концентраций электронов n0 и дырок p0 необходимо знать плотности квантовых состояний в обеих зонах и вероятности заполнения каждого квантового состояния.
Плотность квантовых состояний
Электроны вблизи дна зоны проводимости ведут себя как свободные частицы, если им приписать эффективную массу m*n .
Рассмотрим
плотность квантовых состояний для
электронов в зоне проводимости в
предположении, что эффективная масса
электронов m*n – скаляр. Закон дисперсии для электронов
в зоне проводимости (2.8) E( )=
)= совпадает с законом дисперсии для
электронов в модели Зоммерфельда. Тогда
плотность квантовых состояний в зоне
проводимости gn(E):
gn(E)=
совпадает с законом дисперсии для
электронов в модели Зоммерфельда. Тогда
плотность квантовых состояний в зоне
проводимости gn(E):
gn(E)=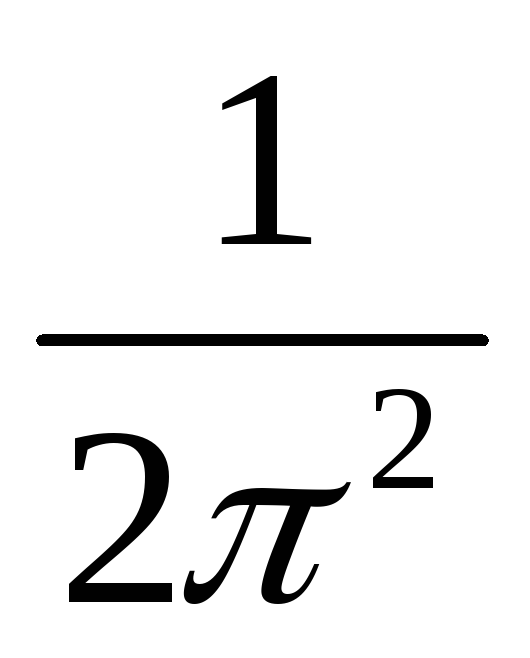 (
(  )
)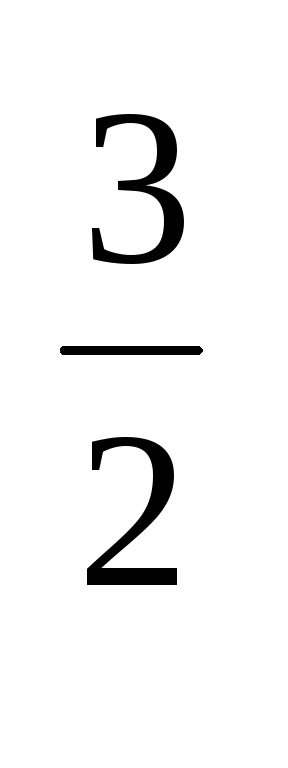 (E-Ec)
(E-Ec) В общем случае эффективная масса
электрона является тензором второго
ранга и описывается тремя компонентами:
m*1 , m*2 , m*3,
а числа эквивалентных минимумов в зоне
проводимости равно Mc>1.
Расчёт даёт выражение
gn(E)=
В общем случае эффективная масса
электрона является тензором второго
ранга и описывается тремя компонентами:
m*1 , m*2 , m*3,
а числа эквивалентных минимумов в зоне
проводимости равно Mc>1.
Расчёт даёт выражение
gn(E)= (
( 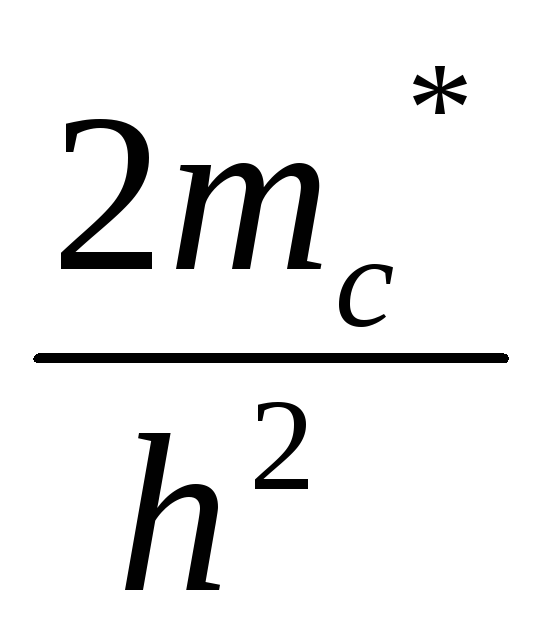 )
) (E-Ec)
(E-Ec)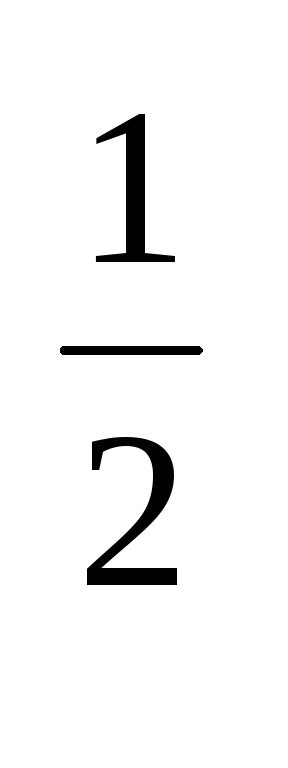 , где mc=
, где mc= – эффективной
массой плотности состояний для электронов.
– эффективной
массой плотности состояний для электронов.
В кремнии в 1 и зоне Бриллюэна имеется шесть минимумов энергии: Мс = 6, а компоненты тензора эффективной массы m*1 =m*2 = m*t =0,19m, m*3=m*l=0,98m Отсюда mc = 1,08m
Аналогично
рассчитывается плотность квантовых
состояний gр(Е)
для дырок в валентной зоне. Полагая
началом отсчёта энергии потолок валентной
зоны и считая эффективную массу дырок
скаляром, получаем валентной зоны и
gp(E)= (
( 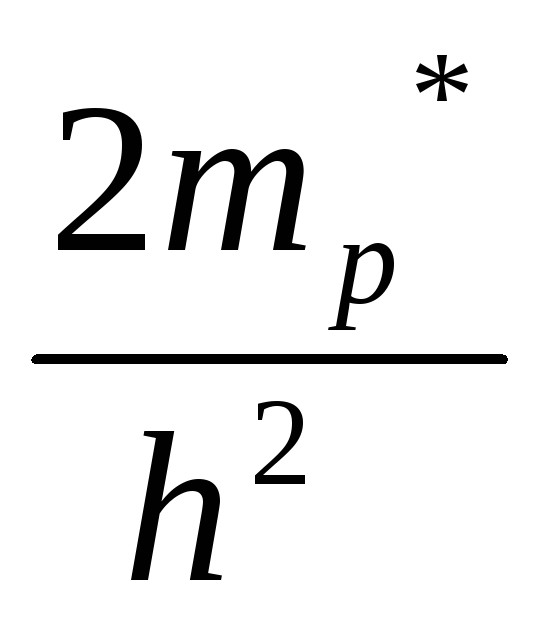 )
)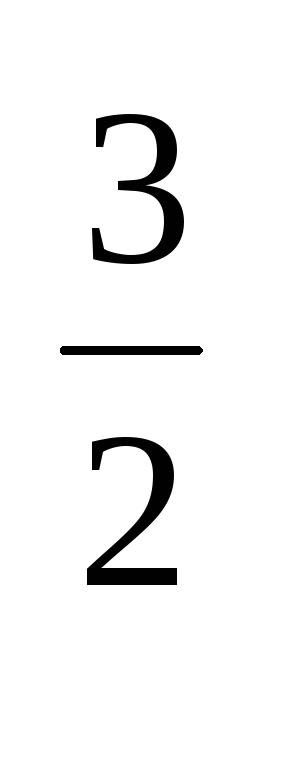 (E
(E -E)
-E)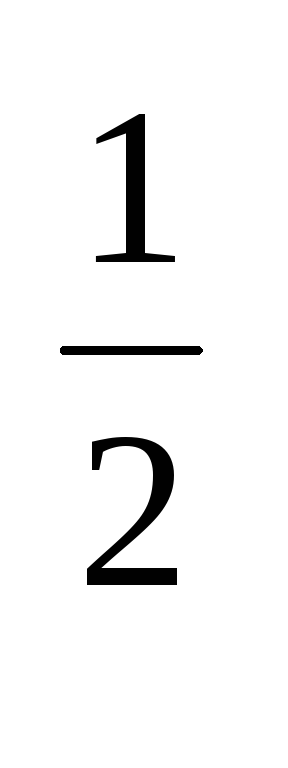 При сложном строении валентной зоны
аналогично можно ввести массу плотности
состояний m
При сложном строении валентной зоны
аналогично можно ввести массу плотности
состояний m для дырок. Например, в кремнии имеются
два вида дырок в валентной зоне с
эффективными массами m*pл = 0,16m
и m*pt = 0,49m.
Для них можно ввести mv=(
m*pл
для дырок. Например, в кремнии имеются
два вида дырок в валентной зоне с
эффективными массами m*pл = 0,16m
и m*pt = 0,49m.
Для них можно ввести mv=(
m*pл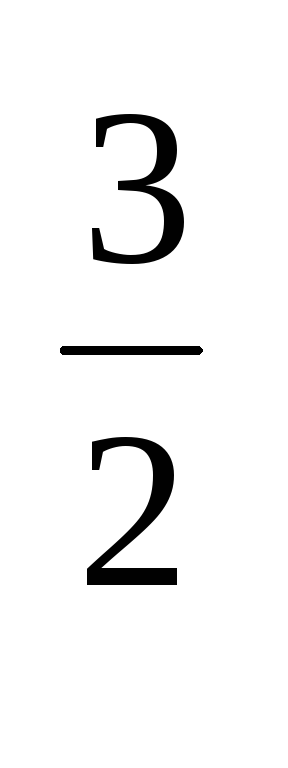 +
m*pt
+
m*pt )
) =0,56m
При этом плотность квантовых состояний
для дырок в валентной
=0,56m
При этом плотность квантовых состояний
для дырок в валентной
зоне
запишется в виде gn(E)=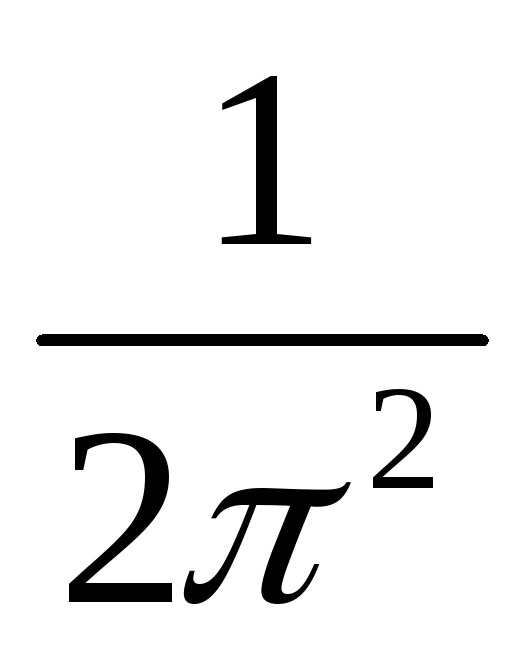 (
(  )
)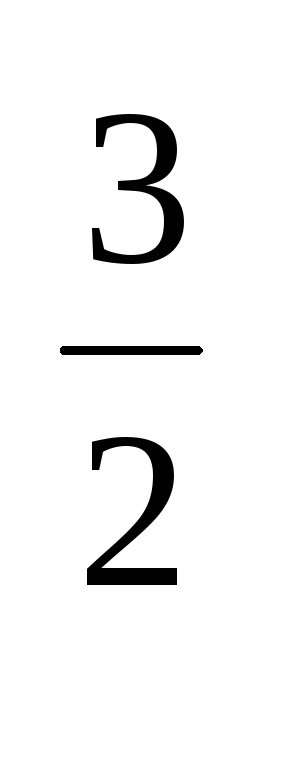 (E
(E -E)
-E)
Функция распределения
В
качестве основной функции, применяемой
при статистическом методе описания,
выступает функция
распределения,
которая определяет
статистические характеристики
рассматриваемой системы.
Функция распределения дает возможность
рассчитывать все наблюдаемые
термодинамические параметры системы.
Рассмотрим какую-либо макроскопическую
систему, состояние которой описывается
некоторым параметром 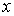 ,
принимающим
,
принимающим дискретных
значений:
дискретных
значений: ,
, ,
…,
,
…,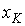 .
Пусть при проведении над системой
.
Пусть при проведении над системой измерений
были получены следующие результаты:
значение
измерений
были получены следующие результаты:
значение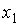 наблюдалось
при
наблюдалось
при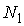 измерениях,
значение
измерениях,
значение наблюдалось
соответственно при
наблюдалось
соответственно при измерениях
и т.д. При этом, очевидно, что общее число
измерений
измерениях
и т.д. При этом, очевидно, что общее число
измерений равняется
сумме всех измерений
равняется
сумме всех измерений ,
в которых были получены значения
,
в которых были получены значения :
: . Увеличение
числа проведенных экспериментов до
бесконечности приводит к стремлению
отношения
. Увеличение
числа проведенных экспериментов до
бесконечности приводит к стремлению
отношения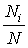 к
пределу
к
пределу 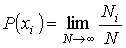 . Величина
. Величина  называетсявероятностью
измерения значения
называетсявероятностью
измерения значения  .
Вероятность
.
Вероятность принимает значения в интервале
принимает значения в интервале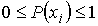 .
Значение
.
Значение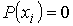 – ни при одном измерении не наблюдается
значение
– ни при одном измерении не наблюдается
значение ,
т.е. система не может иметь состояние,
характеризующееся параметром
,
т.е. система не может иметь состояние,
характеризующееся параметром .
Вероятность
.
Вероятность – при всех измерениях наблюдалось
только значение
– при всех измерениях наблюдалось
только значение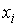 ,т.е.система
находится в детерминированном состоянии
с параметром
,т.е.система
находится в детерминированном состоянии
с параметром .
. 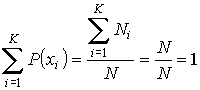 (5.2) Условие (5.2) указывает на то, что если
набор возможных дискретных значений
(5.2) Условие (5.2) указывает на то, что если
набор возможных дискретных значений  ,
, ,
является полным, то при любых измерениях
параметра
,
является полным, то при любых измерениях
параметра должны
наблюдаться значения этого параметра
только из указанного набора
должны
наблюдаться значения этого параметра
только из указанного набора .
Такие параметры как температура,
давление, внутренняя энергия и т.д.,
обычно принимают непрерывный ряд
значений. Переменные, характеризующие
движение микрочастиц (координата и
скорость), изменяются непрерывным
образом.
.
Такие параметры как температура,
давление, внутренняя энергия и т.д.,
обычно принимают непрерывный ряд
значений. Переменные, характеризующие
движение микрочастиц (координата и
скорость), изменяются непрерывным
образом.
Рассмотрим
статистическое описание, когда измеренный
параметр  принимает
значения
принимает
значения .
Причем, параметр
.
Причем, параметр может
изменяться от
может
изменяться от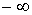 до
до ( координаты молекулы газа для случая
неограниченной среды). Пусть в результате
измерений установлено, что величина
( координаты молекулы газа для случая
неограниченной среды). Пусть в результате
измерений установлено, что величина с
вероятностью
с
вероятностью попадает
в интервал значений от
попадает
в интервал значений от до
до .
Тогда функция
.
Тогда функция характеризуюет плотность распределения
вероятностей:
характеризуюет плотность распределения
вероятностей:  Это
– функцией
распределения.
Это
– функцией
распределения.  должна
удовлетворять условию:
должна
удовлетворять условию: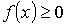 .
Вероятность того, что измеренное значение
попадет в интервал
.
Вероятность того, что измеренное значение
попадет в интервал равна
равна  .
Тогда
.
Тогда 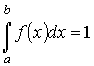 (5.5)
(5.5)
Выражение(5.5)–условие
нормировки функции распределения. позволяет
определить среднее значение любой
функции
позволяет
определить среднее значение любой
функции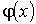 :
:  (5.6) Если
состояние системы характеризуется
двумя параметрами
(5.6) Если
состояние системы характеризуется
двумя параметрами 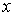 и
и ,
то вероятность её нахождения в состоянии
со значениями этих параметров в интервалах
,
то вероятность её нахождения в состоянии
со значениями этих параметров в интервалах и
и соответственно
равна
соответственно
равна  ,
где
,
где 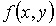 –
двумерная функция распределения.
Примером такой функции может служить
совместное распределение для координат
и скоростей молекул газа. Для бесконечно
малых интервалов
–
двумерная функция распределения.
Примером такой функции может служить
совместное распределение для координат
и скоростей молекул газа. Для бесконечно
малых интервалов и
и вероятность
вероятность можно
представить в виде
можно
представить в виде  .В
случае статистической независимости
значений параметров
.В
случае статистической независимости
значений параметров 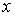 и
и друг
от друга двумерная функция распределений
друг
от друга двумерная функция распределений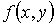 равна
произведению функций распределения
равна
произведению функций распределения и
и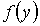 :
: 
studfile.net