- Найти длину диагонали и углы прямоугольника
- выравнивание величины прямоугольника и расчет
- Как проверить прямой угол без угольника
- Прямоугольник – Формулы | Свойства
- Диагональ — Математическая энциклопедия
- диагоналей прямоугольника с калькулятором
- Диагональ прямоугольника. Калькулятор
- Диагоналей квадрата с калькулятором – Math Open Reference
Найти длину диагонали и углы прямоугольника
Диагонали прямоугольника равны между собой. Диагональ делит прямоугольник на два равных прямоугольных треугольника ABC и ACD. Диагональ равна диаметру описанной окружности.
1. Формулы длины диагонали в прямоугольнике.
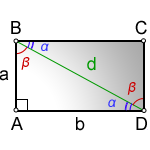
d – диагональ прямоугольника
a, b – стороны
α, β – углы полученные от деления, диагональю, прямого угла
Формула диагонали через стороны, (d):
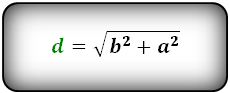
Формулы диагонали через сторону и угол, (d):
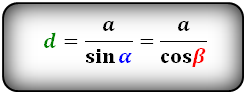
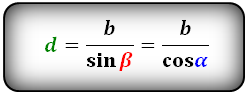
Формулы величины углов через диагональ и стороны, (α, β):


2. Формулы углов между диагоналями в прямоугольнике.

d – диагонали прямоугольника
a, b – стороны
α, β – углы между диагоналями
Формулы углов между диагоналями через стороны и диагональ, (α, β ):


- Подробности
- Автор: Administrator

Скачать, сохранить результат
Выберите способ сохранения
Информация
Профессиональное проектирование и формирование фундамента, стен, а также полноценной системы крыши дома требует чёткого выставления геометрических углов и расчёта диагоналей сегментов конструкций. От точности вычислительных манипуляций напрямую зависит безопасность, устойчивость, прочность и долговечность здания. Интерактивный калькулятор диагоналей для расчёта фундамента и крыш поможет безошибочно выполнить все расчётные операции на этапе проектирования дома всего за несколько секунд.
Преимущества калькулятора диагоналей
- Помогает безошибочно рассчитать квадрат конкретной секции фундамента всего в несколько кликов.
- Позволяет самостоятельно выполнить расчёт диагонали прямоугольника или треугольника.
- Помогает быстро рассчитать общую длину и ширину фундамента, а также стен дома.
- Результаты расчётных операций гарантируют чёткое выставление геометрических углов в 90° при монтаже конструкционных элементов фундамента, стен и крыши.
- Экономит уйму времени, сил нервов и средств в процессе проектирования строений всех категорий.
- Расчёт диагоналей основания обеспечивает безупречное обустройство фундамента, что дарит дому безопасность, надёжность и долговечность.
- Возможность бесплатно получить результаты расчётных операций в формате PDF на свой E-mail или мгновенно распечатать их в режиме онлайн.
Безошибочно рассчитайте геометрические параметры фундамента, стен и конструкционных элементов системы крыши уже сегодня. Бесплатно задействуйте онлайн калькулятор диагоналей — сэкономьте силы, время и деньги прямо сейчас!
поделиться и оценить
Смотрите также:
Добавить комментарий
выравнивание величины прямоугольника и расчет
Содержание статьи:
После окончания проектирования размеры опоры строения переносятся на участок строительства. От качественной разметки зависит равномерность фундамента и правильное выставление отметок для возведения постройки. Чтобы сделать углы точно под 90°, проверяют диагонали фундамента и сравнивают их между собой. Если все сделано правильно, надземная часть будет прочной и не деформируется со временем.
Необходимость расчета диагонали фундамента
При неверном расчете диагонали все дальнейшее строительство будет расходиться с планом
Проект предполагает подбор конструктивных элементов точно в размер, чтобы при строительстве не возникало перекосов. Длина балки или плиты перекрытия берется с требуемой глубиной опирания, которая принимается по конструктивному расчету. Во время разметки фундамента нужна предельная точность, т.к. отклонение в размерах повлечет расхождение вертикальных конструкций.
Горизонтальные элементы могут не влезть в проектное положение или вываливаться из монтажного пространства, поэтому потребуется перерасчет длины, а также других показателей.
Правильная разметка основания ведет к приятным бонусам при возведении здания:
- простота строительства стен и применения сборных элементов;
- соблюдение предусмотренной проектом экономии средств и материалов;
- сооружение объекта без отклонений от проекта.
Перед тем как вымерить диагональ фундамента, нужно выровнять строительную площадку, чтобы удобно было размечать линии на местности. Почти всегда строительные конструкции и материалы от утеплительных матов до досок и стеновых щитов имеют прямые углы, поэтому фундамент также размечают с учетом этих требований.
Если диагонали прямоугольника оказываются равными, геодезист выполнил идеальную разметку. Если диагонали неодинаковые, спроектирован не прямоугольник. Но у равнобедренной трапеции также получаются диагонали одинаковой длины, поэтому проверяют стороны угла по принципу золотого сечения с помощью длинного шнура и рулетки.
Сложности при неправильной разметке

Нарушение геометрии фундамента снижает прочность стен
Неправильная переноска размеров на местность и пренебрежение сравнением диагоналей приведет к тому, что на поверхности земли появится ромб или трапеция. При устройстве самого фундамента это может и не станет заметно, но первая укладка плит над подвалом выявит несоответствия и приведет к потерям времени для перерасчета сборных элементов или переделке основания.
Если плита опирается меньше требуемой глубины, после получения нагрузки от оборудования или людей она может обломить опорную часть стены и упасть. Такая неприятность коснется горизонтальных элементов перекрытия на всех этажах высотного строения и будет повторяться вплоть до кровли.
Выполнить устройство крыши трудно, если не соответствуют размеры между балками, фермы приходится ставить большего размера, а в других местах уменьшать габариты. Увеличивается трудоемкость работ, т.к. исполнитель выступает в несвойственной для него роли конструктора и проектировщика.
Усложнится установка кровельного покрытия, т.к. листы профнастила или шифера выпускаются с прямыми углами. Сборные угловые элементы водоотлива также рассчитаны на установку под 90°, желоб будет отходить от края кровли, а вода попадет на вертикальные ограждения, стены будут отсыревать.
Сложности возникнут с последующими работами, поэтому нужно проверить диагональ фундамента и сравнить результаты. Аналогично проводят измерения после установки опалубки, чтобы подтвердить правильность расчетов.
Правильный расчет диагонали фундамента
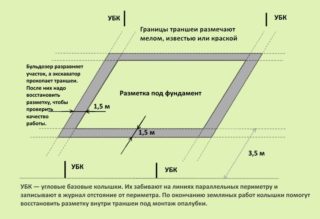 После изучения плана основания нужно приступать к разметке одной из сторон. Это может быть боковая часть, фасадная или задняя, в данном случае это не является важным условием, т.к. принимается во внимание только ориентирование направления.
После изучения плана основания нужно приступать к разметке одной из сторон. Это может быть боковая часть, фасадная или задняя, в данном случае это не является важным условием, т.к. принимается во внимание только ориентирование направления.
Длина фундаментной стены не учитывается, можно взять на 1,0 метр больше от места предстоящих углов. В этих точках забивают колья, и натягивают шпагат. Запас по длине дается, чтобы при копке траншеи не вытащить колышек, и он остался для обозначения направления стороны.
Колышки заменяют доской длиной 1 – 2 метра с прибитыми кольями в торце. Привязанный к ним шнур можно оперативно передвигать из стороны в сторону при необходимости. Такое приспособление для работы называют обноской, оно позволяет расчертить участок с точностью до нескольких миллиметров.
Порядок работы:
- После натяжки шпагата находят точку отсчета по длине и определяют угол фундамента, на шпагате в этой точке цепляют прищепку или забивают кол в грунт, так появляется 2 угла.
- Идентично поступают с перпендикулярной стороной и определяют направление.
- Перед тем как рассчитать диагональ прямоугольного треугольника, по сторонам откладывают 3 и 4 равные части, отмечают их на шпагате (например, 3 и 4 метра).
- Зависимость расстояния между отмеченными точками такова, что гипотенуза должна быть равна пяти частям (5 метров) и не отличаться даже сантиметром, иначе пойдет скос.
Сразу трудно получить правильный результат разметки. Расстояние меньше пяти частей будет означать острый угол, а больше — говорить о величине, превышающей 90°.
Необходимые инструменты для работы
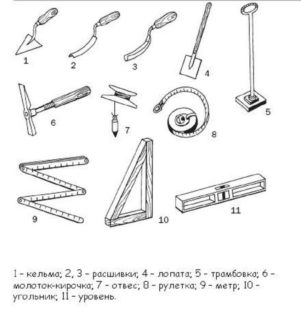
Инструменты для разметки фундамента
Во время рытья траншей экскаватором убирают шнуры, которые натянуты с выносом от углов, а места сторон отмечают на грунте посыпкой контрастным веществом, например, светлым песком или мелом. Элементы обноски красят яркой краской, чтобы экскаваторщик мог их увидеть и не наехать на разметочные части. После рытья траншеи шнуры натягивают на старое место и проверяют расположение ям или котлованов.
Расчет диагонали фундамента ведется с применением инструментов и приспособлений:
- колья из древесины или ровной арматуры, без кривизны;
- ровные куски металлического профиля или сухой рейки по 2 – 2,5 метра для горизонтального переноса точек;
- капроновый шнур или крепкий шпагат;
- гвозди, шурупы или саморезы;
- угольник, рулетка, молоток, ножницы;
- отвес, водяной или лазерный уровень.
Геодезисты используют теодолит, чтобы размечать углы и давать отметки по высоте. У частников нет такого инструмента, для работы с ним требуется навык. Правильно измерить диагональ дома можно с помощью простых приспособлений.
На угольник закрепляют лазерные указки и строительный уровень — такое приспособление покажет высокую точность при разметке. Продаются транспортиры и угольники большого размера, лучше взять такие, чтобы было удобнее переносить линии плана на местность. Первоначальная разметка очень важна для начала строительства, поэтому желательно высчитать диагональ несколько раз, чтобы быть уверенным в правильности работы.
Выравнивание величины прямоугольника
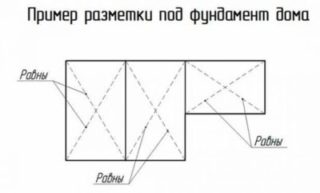 В прямоугольнике все углы должны равняться 90°, иначе получится неравнобедренная фигура с перекосами стен. Абрис фундамента имеет наружную и внутреннюю сторону, поэтому требование к прямоугольности касается обоих контуров. Легче всего выровнять величину для дома простой прямоугольной формы, который имеет четыре стены.
В прямоугольнике все углы должны равняться 90°, иначе получится неравнобедренная фигура с перекосами стен. Абрис фундамента имеет наружную и внутреннюю сторону, поэтому требование к прямоугольности касается обоих контуров. Легче всего выровнять величину для дома простой прямоугольной формы, который имеет четыре стены.
Иногда фундаменты в плане имеют сложное строение, например, делаются дополнительные монолитные ленты под пристройку или веранду, а каминный зал рассматривается как вынесенное помещение. В таком случае разметка усложняется тем, что площадь дома будет складываться из отдельных прямоугольников, которые размечаются отдельно.
Каждая фигура после распланировки поверяется на соответствие с другими частями и между составными элементами также устанавливаются прямые углы. Первоначальная сторона привязывается к какой-нибудь основе на местности, которая выглядит прямолинейно. Это может быть ограда, забор, трамвайные пути или бордюр асфальтированной трассы. От этой линии откладывается одинаковое расстояние для обозначения первой стороны искомого плана фундамента.
После окончательной разметки нужно правильно рассчитать диагональ и сравнить расстояние между первой-третьей и второй-четвертой вершиной прямоугольника на местности. Должны получиться идеально одинаковые расстояния. Проверяют и длину противоположных сторон, которые также должны быть равны.
Нахождение третьего и четвертого углов
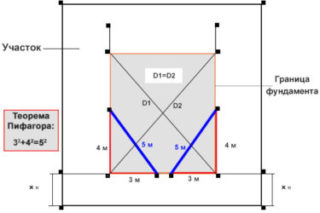
При расчете используется теорема Пифагора
Соответствие частей в треугольнике, по которому размечается прямой угол на участке, можно проверить теоремой Пифагора. Она выражается формулой a² + b² = c²: квадрат гипотенузы равняется сумме квадратов катетов.
Чтобы высчитать длину соединяющей гипотенузы, нужно высчитать квадрат одного расстояния на шнуре с квадратом другой стороны угла и сложить полученные значения. Из результата следует высчитать квадратный корень, чтобы получить длину гипотенузы. Так можно выровнять диагональ прямоугольника, чтобы получить идеальный прямой угол.
Третий и четвертый углы находятся аналогичным способом по отправной вершине и существующей стороне. После выставления последнего угла проверяется противоположные диагонали и стороны в фигуре для сравнения. Используется шнур, который не растягивается по длине, чтобы не искажать измерения.
Старинный способ измерить диагональ дома предполагает использование бечевки с завязанными на ней 13 узелками на абсолютно равном расстоянии друг от друга. На одну сторону прямоугольника приходилось 3 расстояния между узлами, при этом четвертый совпадал с вершиной угла. После верхушки отмеряли 4 таких отрезка. На гипотенузу приходилось оставшихся 5 промежутков, и первый узел при натяжении должен был совпадать с 13 завязанным элементом.
Как проверить прямой угол без угольника
При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов – длинна сторон не ограничена. Основной инструмент для измерений – рулетка.
Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.
Теорема Пифагора
Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:
a²+b²=c²

Стороны a и b – катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c – гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.
Теорема Пифагора известна еще под названием “египетский треугольник”. Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 – ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 – все сходится!

А теперь применим теорему на практике.
Проверка прямого угла
Начнем с самого простого – проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены – это стены, расположенные друг к другу под прямым углом 90°.
Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 – это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 – 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали – проверяемый угол развернут и имеет отклонение от 90°.

Калькулятор расчета диагонали прямого угла
Извлечение квадратного корня никогда меня не привлекало – простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. – диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике – это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем – в некоторых случаях он очень актуален.

Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.
Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.

Как разметить прямой угол рулеткой
Разметка может основываться как на общей теореме Пифагора, так и на принципе “египетского треугольника”. Однако это только в теории линии просто чертятся на бумаге, “ловить” же все выбранные размеры растянутыми шнурами или линиями на полу – задача посложнее.
Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!
Как разметить острый угол
Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами – дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.
Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера – непрофессионально.
Оцените публикацию:Оценка: 4.4 (62 голосов)
Смотрите также другие статьи
Прямоугольник — это параллелограмм, у которого все углы прямые.
Диагонали прямоугольника равны.

1. В прямоугольнике диагональ делит угол в отношении , меньшая его сторона равна . Найдите диагональ данного прямоугольника.

Всё просто. Рассмотрите прямоугольный треугольник . Найдите, чему равен угол и его синус, а затем найдите .
Ответ: .
А сейчас рассмотрим еще одну задачу, в которой применяются свойства диагоналей прямоугольника.
2. Острые углы прямоугольного треугольника равны и . Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Казалось бы, при чем здесь прямоугольник? Дан прямоугольный треугольник, из вершины прямого угла проведены высота и медиана. А что можно сказать о длине этой медианы?
Давайте достроим чертеж до прямоугольника. Поскольку диагонали прямоугольника равны (это свойство прямоугольника) и делятся пополам в точке пересечения, отрезки , и тоже будут равны. Каждый из них равен половине диагонали прямоугольника. Мы доказали теорему:
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Итак, , значит, треугольник равнобедренный, и угол равен .
По свойству высоты, проведенной из вершины прямого угла,
.
Тогда угол (между медианой и высотой треугольника ) равен .
Ответ: .
Как вы думаете, где находится центр окружности, описанной вокруг прямоугольного треугольника? Ведь центр описанной окружности — точка, равноудаленная от всех вершин треугольника. Очевидно, эта точка — середина гипотенузы.
В прямоугольном треугольнике центром описанной окружности является середина гипотенузы.
1. Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен .
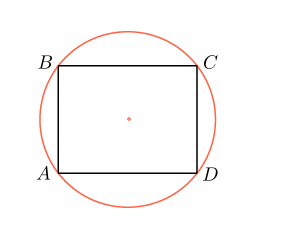
Проведем диагональ .

Получим, что равна .
Ответ: .
Прямоугольник – Формулы | Свойства
Для расчёта всех основных параметров прямоугольника воспользуйтесь калькулятором.
Свойства прямоугольника
- Противоположные стороны прямоугольника равны
- Противоположные стороны прямоугольника параллельны
- Прилегающие стороны прямоугольника всегда перпендикулярны
- Все четыре угла прямоугольника прямые
- Сумма углов прямоугольника равна 360°
- Диагонали прямоугольника одинаковой длины
- Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон $$ 2 * BD^2 = 2 * AB^2 + 2 * BD^2 $$
- Каждая диагональ прямоугольника делит прямоугольник на два равных прямоугольных треугольника
- Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам
- Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
- Диагональ прямоугольника является диаметром описанной окружности
- Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180°
Формулы длин сторон прямоугольника
Длина стороны через диагональ и другую сторону
$$ AD = \sqrt{BD^2 – AB^2} $$ $$ AB = \sqrt{BD^2 – AD^2} $$Длина стороны через площадь (S) и другую сторону
$$ AD = {S \over AB} $$ $$ AB = {S \over AD} $$Длина стороны через периметр (P) и другую сторону
$$ AD = {P – 2 * AB \over 2} $$ $$ AB = {P – 2 * AD \over 2} $$Длина стороны через диагональ и угол ∠ACD
$$ AD = BD * sin(∠ACD) $$ $$ AB = BD * cos(∠ACD) $$Длина стороны через диагональ и угол ∠BOC
$$ AD = BD * sin({∠BOC \over 2}) $$ $$ AB = BD * cos({∠BOC \over 2}) $$Формулы длины диагонали прямоугольника
Длина диагонали прямоугольника через две стороны прямоугольника
$$ BD = \sqrt{AD^2 + AB^2} $$Длина диагонали прямоугольника через площадь (S) и любую сторону
$$ BD = {\sqrt{S^2 + AB^4} \over AB} = {\sqrt{S^2 + AD^4} \over AD} $$Длина диагонали прямоугольника через периметр и любую сторону
$$ BD = {\sqrt{P^2 – 4 * P * AB + 8 * AB^2} \over 2} = {\sqrt{P^2 – 4 * P * AD + 8 * AD^2} \over 2} $$Формулы периметра прямоугольника
Периметр прямоугольника через две стороны
$$ P = 2 * (AB + AD) $$Периметр прямоугольника через площадь (S) и любую сторону
$$ P = {2 * S + 2 * AB^2 \over AB} = {2 * S + 2 * AD^2 \over AD} $$Формулы площади прямоугольника
Площадь прямоугольника через две стороны
$$ S = AB * AD $$Площадь прямоугольника через периметр и любую сторону
$$ S = {P * AB – 2 * AB^2 \over 2} = {P * AD – 2 * AD^2 \over 2} $$Формулы радиуса описанной окружности прямоугольника
Радиус описанной окружности через диагональ
$$ R_O = {BD \over 2} $$Радиус описанной окружности через две стороны
$$ R_O = {\sqrt{AB^2 + AD^2} \over 2} $$Диагональ — Математическая энциклопедия
Отрезок прямой, соединяющий две вершины многоугольника (многогранника), не лежащие на одной стороне (на одной грани). Если число вершин многоугольника равно п, то число его Д. равно п( п-3)/2. Е. В. Шикин.
Источник: Математическая энциклопедия на Gufo.me
Значения в других словарях
- диагональ — ДИАГОНАЛЬ, и, ж. 1. В математике: отрезок прямой линии, соединяющий две вершины многоугольника, не лежащие на одной стороне, или две вершины многогранника, не лежащие на одной грани. 2. Ткань с косыми рубчиками. Толковый словарь Ожегова
- диагональ — По диагонали — наискось, не под прямым углом. ► Перешел улицу по диагонали. Фразеологический словарь Волковой
- диагональ — I. ДИАГОНАЛЬ I и, ж. diagonale f. <, лат. diagonalis <�гр. diagonis идущий от угла к углу. мат. Некоего четвероуголия не равнобочнаго именуемаго паралеллеграмма дан диагональ. Арифм. Магн. 214. // Сл. 18 6 123. Словарь галлицизмов русского языка
- Диагональ — I Диагона́ль (лат. diagonalis, от греч. diagоnios — идущий от угла к углу) 1) Д. многоугольника — отрезок прямой, соединяющий две его вершины, не лежащие на одной стороне. Если число вершин многоугольника n, то число Д. равно n (n — 3)/2. 2)… Большая советская энциклопедия
- диагональ — ДИАГОНАЛЬ ж. черта, соединяющая два угла, проведенная с угла на угол, в плоском угольнике или в теле; искосина, долонь. Долонь прямоуголыника делит его пополам, на два равные треугольника. || Род французского сукна, с косою низкою. Толковый словарь Даля
- диагональ — Диагональ, диагонали, диагонали, диагоналей, диагонали, диагоналям, диагональ, диагонали, диагональю, диагоналями, диагонали, диагоналях Грамматический словарь Зализняка
- Диагональ — См. Переплетение нитей в тканях. Энциклопедический словарь Брокгауза и Ефрона
- диагональ — ДИАГОНАЛЬ 1. В настольном теннисе — направление полета мяча из одного угла стола в другой, диаметрально противоположный. Напр., из левого угла стола игрока в левый угол стола соперника. Словарь спортивных терминов
- диагональ — 1) (звёздная диагональ) Приставка к небольшому телескопу, содержащая маленькое плоское зеркало или призму. Используются, чтобы повернуть луч света под прямым углом в направлении тубуса, в который вставлен окуляр. Большой астрономический словарь
- диагональ — Немецкое – Diagonale. Французское – diagonale. Латинское – diagonalis (диагональная линия). Слово «диагональ» пришло в русский язык из западноевропейских языков, скорее всего, из немецкого. Этимологический словарь Семёнова
- диагональ — орф. диагональ, -и Орфографический словарь Лопатина
- диагональ — Диагонали, ж. [латин. diagonalis]. 1. Прямая линия, соединяющая несмежные вершины многоугольника или многогранника (мат.). || То же спец. о прямой линии, соединяющей противоположные углы прямоугольника и расположенной под острым углом к его сторонам (мат. Большой словарь иностранных слов
- ДИАГОНАЛЬ — ДИАГОНАЛЬ — плотная хлопчатобумажная или шерстяная ткань с отчетливо выраженными наклонными рубчиками. Из диагонали шьют воинское обмундирование, куртки и т. д. ДИАГОНАЛЬ (от греч. Большой энциклопедический словарь
- диагональ — диагональ , -и Орфографический словарь. Одно Н или два?
- диагональ — ДИАГОНАЛЬ 1. ДИАГОНАЛЬ, -и; ж. [лат. diagonalis] 1. Матем. Отрезок прямой, соединяющий две несмежные вершины многоугольника или две вершины многогранника, не принадлежащие одной грани. Д. квадрата. Д. октаэдра. Разделить квадрат диагональю. Провести д. Толковый словарь Кузнецова
- диагональ — сущ., кол-во синонимов: 6 долонь 6 искосина 4 косек 5 линия 182 спецдиагональ 1 ткань 474 Словарь синонимов русского языка
- диагональ — -и, ж. 1. мат. Отрезок прямой, соединяющий вершины двух несмежных углов многоугольника или две вершины многогранника, не лежащие в одной плоскости. 2. Плотная ткань с рубчиками, идущими по косой линии. Малый академический словарь
- диагональ — диагональ I ж. Отрезок прямой линии, соединяющий две несмежные вершины многоугольника, не лежащие на одной стороне или две вершины многогранника, не принадлежащие одной грани (в математике). II ж. Толковый словарь Ефремовой
- диагональ — Диагона́ль/. Морфемно-орфографический словарь
- диагональ — ДИАГОН’АЛЬ, диагонали, ·жен. (·лат. diagonalis). 1. Прямая линия, соединяющая несмежные вершины многоугольника или многогранника (мат.). | То же спец. Толковый словарь Ушакова
- диагональ — диагона́ль ж., из франц. diagonale; см. Горяев, ЭС 4461. •• 1 У Горяева так: из лат. diagōn-āl-is (греч. διαγων-ια). — Прим. ред. Этимологический словарь Макса Фасмера
- Диагональ — Плотная ткань с рельефными наклонными рубчиками на лицевой стороне. Вырабатывается чистошерстяная, полушерстяная, хлопчатобумажная, шелковая, штапельная ткань. Используется для шитья мужских костюмов, форменной одежды и спецодежды. (Энциклопедия моды. Андреева Р., 1997) Энциклопедия моды и одежды

диагоналей прямоугольника с калькулятором
Диагонали прямоугольника с калькулятором – Math Open ReferenceПопробуй это Перетащите любую вершину прямоугольника ниже. Он останется прямоугольником, и длина диагонали будет рассчитана.
Прямоугольник имеет две диагонали. Каждый является отрезок проведено между противоположным вершины (углы) прямоугольника. Диагонали имеют следующие свойства:
- Две диагонали конгруэнтный (такой же длины).На рисунке выше нажмите «показать обе диагонали», затем перетащите оранжевую точку в любую вершину прямоугольника и убедитесь, что это так.
- каждая диагональ рассекает другой. Другими словами, точка, где диагонали пересекаются (крест), делит каждую диагональ на две равные части
- Каждая диагональ делит прямоугольник на две конгруэнтные прямоугольные треугольники. Поскольку треугольники являются конгруэнтными, они имеют одинаковую площадь, и каждый треугольник имеет половину площади прямоугольника.
Длина диагонали
На рисунке выше нажмите «сброс».Как видите, диагональ прямоугольника делит его на две части. прямоугольные треугольники, BCD и DAB. Диагональ прямоугольника – это гипотенуза из этих треугольников. Мы можем использовать Теорема Пифагора найти длину диагонали, если мы знаем ширину и высоту прямоугольника.
Как формула: где:w – ширина прямоугольника
h – высота прямоугольника
Калькулятор
Используйте калькулятор выше, чтобы рассчитать свойства прямоугольника.
Введите две стороны длины, а остальные будут рассчитаны. Например, введите две длины сторон. Площадь, периметр и длина диагонали будут найдены.
Что попробовать
- На рисунке вверху страницы нажмите «Сброс» и «Скрыть детали». Затем перетащите углы, чтобы создать произвольный прямоугольник. Рассчитайте длину диагоналей. Нажмите «показать детали», чтобы подтвердить свой ответ.
- Прямоугольник имеет высоту 12 и диагональ 31.Найдите ширину прямоугольника и используйте анимацию или калькулятор выше, чтобы проверить свой ответ.
Другие темы многоугольника
General
Типы полигонов
Площадь различных типов полигонов
Периметр различных типов многоугольников
Углы, связанные с полигонами
Именованные полигоны
(C) 2011 Copyright Math Открытая ссылка.
Все права защищены
Диагональ прямоугольника. Калькулятор
Наш калькулятор диагонали прямоугольника – это обширный инструмент, который быстро находит диагональ и другие параметры прямоугольника. Встречались ли вы с конкретной проблемой прямоугольника, и вы не знаете , как найти диагональ прямоугольника ? Попробуйте ввести пару параметров в поля рядом с текстом или продолжайте чтение, чтобы узнать, какова возможная диагональ формулы прямоугольника .
Вы можете увидеть типичный прямоугольник на рисунке ниже.Мы отметили пять основных величин, которые описывают определенный прямоугольник. Вы можете использовать их, чтобы получить диагональ формулы прямоугольника. Это:

- л – длина ,
- Вт – ширина ,
- α – угол между диагоналями ,
- р – радиус окружности ,
- d – диагональ ,
и два других параметра, которые не показаны на рисунке:
Термин прямоугольник происходит от латинского rectangulus , который представляет собой комбинацию двух слов: rectus (справа, правильно) и angulus (угол).Это название происходит от того факта, что прямоугольник представляет собой четырехугольник с четырьмя прямыми углами (4 * 90 ° = 360 °). Его противоположные стороны параллельны и имеют одинаковую длину, а две его диагонали пересекаются друг с другом посередине и также имеют одинаковую длину.
Квадрат – это особый случай прямоугольника. Его определение состоит в том, что он имеет все четыре стороны равной длины, или, альтернативно, угол между двумя диагоналями является прямым. Попробуйте наши калькуляторы, посвященные квадратам. Они могут быстро оценить периметр, площадь и диагональ каждого квадрата, который вы хотите, только по длине его стороны.
Центр прямоугольника равноудален от его вершин, и поэтому вы можете всегда описывать окружность . С другой стороны, вы можете вписать круг в прямоугольник, только если это квадрат .
Диагоналей квадрата с калькулятором – Math Open Reference
Диагонали квадрата с калькулятором – Math Open ReferenceПопробуй это Перетащите любую вершину квадрата ниже. Он останется квадратным, и длина диагонали будет рассчитана.
Квадрат имеет две диагонали. Каждый является отрезок проведено между противоположным вершины (углы) квадрата. Диагонали имеют следующие свойства:
- Две диагонали конгруэнтный (такой же длины).На рисунке выше нажмите «показать обе диагонали», затем перетащите оранжевую точку в любую вершину квадрата и убедитесь, что это так.
- каждая диагональ рассекает другой. Другими словами, точка, где диагонали пересекаются (крест), делит каждую диагональ на две равные части
- Каждая диагональ делит квадрат на две конгруэнтный равнобедренный прямоугольные треугольники Поскольку треугольники совпадают, они имеют одинаковые площадь, и каждый треугольник имеет половину площади квадрата.
Длина диагонали
На рисунке выше нажмите «сброс». Как видите, диагональ квадрата делит его на две части. прямоугольные треугольники, BCD и DAB. Диагональ квадрата – это гипотенуза из этих треугольников. Мы можем использовать Теорема Пифагора найти длину диагонали, если мы знаем длину стороны квадрата.
Как формула: где с – длина любой стороны, которая упрощается до:
Калькулятор
Используйте калькулятор выше, чтобы рассчитать свойства квадрата.
Введите любое одно значение, а остальные три будут рассчитаны. Например, введите длину стороны, и диагональ будет рассчитана.
Точно так же, если вы введете область, будет вычислена длина стороны, необходимая для получения этой области.
Координатная геометрия
Если вы знаете координаты из вершины квадрат, вы можете рассчитать все другие свойства, в том числе диагональные длины. Подробнее об этом смотрите Квадрат (Координатная геометрия)Что попробовать
На рисунке в верхней части страницы нажмите «Сброс» и «Скрыть детали».Затем перетащите любой угол, чтобы создать произвольный квадрат. Рассчитайте длину диагоналей. Нажмите «показать детали», чтобы подтвердить свой ответ.Другие темы многоугольника
General
Типы полигонов
Площадь различных типов полигонов
Периметр различных типов многоугольников
Углы, связанные с полигонами
Именованные полигоны
(C) 2011 Copyright Math Открытая ссылка.
Все права защищены
Диагональ – это сегмент, который соединяет две непоследовательные вершины в многоугольнике. Число диагоналей в многоугольнике , которые можно нарисовать из любой вершины многоугольника, на три меньше числа сторон. Чтобы найти общее количество диагоналей в многоугольнике, умножьте количество диагоналей на вершину (n – 3) на количество вершин n и разделите на 2 (в противном случае каждая диагональ считается дважды).
Сколько диагоналей многоугольника с 300 сторонами? Ну, не имеет большого смысла рисовать многоугольник с 300 сторонами и рисовать на всех этих диагоналях. Должен быть ярлык или формула.
Хорошо, сначала давайте вернемся. Что такое диагональ? Диагональ – это любой отрезок, соединяющий две непоследовательные вершины. Так что, если мы посмотрим на треугольник. Если я посмотрю на каждую отдельную вершину, снова вершина, где два конца встречаются, встречаются две стороны.Я не могу нарисовать диагональ здесь, потому что для этой вершины обе эти стороны являются последовательными. Поэтому у нас нет возможности иметь какие-либо диагонали.
Однако, если я посмотрю на квадрат, я увижу, что есть одна непоследовательная вершина, если я посмотрю на эту вершину. Я смотрю на другую вершину, есть только одна непоследовательная вершина. Итак, давайте посмотрим, сможем ли мы выяснить шаблон. Для этого мы будем использовать эту таблицу здесь, где у меня есть три столбца; один для числа вершин, один для числа диагоналей на вершину и общего числа диагоналей, которые мы видим в многоугольнике.
Итак, мы уже начали с двух разных полигонов. Мы говорили о треугольнике. Итак, количество вершин в треугольнике – это всего три. Мы сказали, что число диагоналей равно нулю, потому что у нас нет возможности рисовать по диагонали. Что означает, что наши общие диагонали все еще равны нулю. Ладно?
Давайте вернемся и посмотрим на площадь. В квадрате мы сказали, что есть 1, 2, 3, 4 вершины. Эта вершина прямо здесь имеет только одну диагональ, эта вершина прямо здесь имеет только одну диагональ, поэтому мы имеем четыре вершины, каждая вершина имеет одну диагональ, но мы видим только две из них.Итак, мы видим, что здесь должно произойти какое-то разделение.
Наконец, давайте посмотрим на пятиугольник. Если я посмотрю на эту вершину, я смогу нарисовать одну, две диагонали. И я увижу, что для каждой вершины я смогу нарисовать две разные диагонали. Таким образом, число вершин здесь равно пяти, число диагоналей на одну вершину равно двум, и общее количество диагоналей здесь у нас есть маленькая звезда, поэтому у нас есть пять диагоналей. Итак, я хочу знать сначала для n вершин, потому что я собираюсь нарисовать точку точка точка для n вершин, каково будет общее число?
Хорошо, я вижу, что если я умножу 3 раза на 0, то мы сделаем точку здесь.3 раза 0 – это 0, так что все в порядке. Здесь у нас есть 4 раза 1, но это не равно 2. Так что нам нужно будет взять 4 раза 1 и разделить это пополам. 5, умноженное на 2, разделенное пополам, равно 5. Итак, я смотрю на количество вершин, которые у нас есть три, поэтому мы будем называть это n. Здесь у нас есть число диагоналей на вершину, здесь у нас есть 0, 1 и 2, и я вижу, что, чтобы получить от 3 до 0, я собираюсь вычесть 3, чтобы получить от 5 до 1, я вычесть 3 из 5 из 2, вычесть 3. Таким образом, у нас есть n раз количество n минус 3 все делится на 2.
Итак, две ключевые вещи об этой формуле, которая говорит вам количество диагоналей, и я собираюсь сокращать DIAG.
Итак, количество диагоналей, я хочу отметить две ключевые вещи. Первый это н-3. Откуда n-3? Хорошо, если у нас есть пять вершин здесь. Мы не собираемся считать саму вершину, потому что вы не можете нарисовать вершину к себе, плюс есть еще две последовательные вершины для общего количества трех вершин в этом многоугольнике, которые мы на самом деле не считаем.
Вторая ключевая часть – это деление на 2. Почему мы должны делить это на 2? Если я вернусь к этому квадрату, если я посмотрю на эту вершину, я нарисовал одну диагональ. С точки зрения этой вершины, я только нарисовал одну. С точки зрения этой вершины я нарисовал другую диагональ. Но это такая же диагональ. Таким образом, каждая вершина и каждая диагональ, которую мы рисуем из вершины, будут учитываться дважды, поэтому мы должны разделить нашу формулу на два.

