- формулы для расчета, свойства и нахождение через диаметр
- Прямоугольник. Формулы и свойства прямоугольника
- Как найти диагональ прямоугольника — mathsathome.com
- Как найти диагональ прямоугольника Видеоурок:
- Как найти диагональ прямоугольника с помощью теоремы Пифагора
- Формула для нахождения диагонали прямоугольника
- Калькулятор диагонали прямоугольника
- Как найти диагональ квадрата
- Как найти диагональ прямоугольника, зная площадь
- Как найти диагональ прямоугольника по периметру
- Как найти длину диагонали ромба?
формулы для расчета, свойства и нахождение через диаметр
Геометрия
12.11.21
7 мин.
При решении задач по физико-математическим дисциплинам иногда необходимо найти диагонали прямоугольника. Формула в интернете не всегда является достоверной. Очень важно на начальных стадиях вычислений правильно идентифицировать фигуру, чтобы применить к ней нужные свойства и соотношения. Специалисты рекомендуют не приступать сразу к практике, а разобраться с теорией.
Оглавление:
- Общая информация
- Формулы и соотношения
- Пример расчета параметров
Прямоугольник — геометрическая плоская фигура, состоящая из четырех попарно параллельных сторон, между которыми образованы прямые углы. Ее можно перепутать с квадратом, имеющим похожие свойства и тождества. При решении задачи очень важно правильно найти фигуру, имеющую определенные признаки определения. Некоторые учащиеся путают последние со свойствами. Эти два термина отличаются между собой.
Некоторые учащиеся путают последние со свойствами. Эти два термина отличаются между собой.
Методика идентификации
Признак — совокупность некоторых критериев, позволяющих правильно различать фигуры. Прямоугольник возможно идентифицировать по таким правилам:
- Неравенство сторон, являющихся смежными.
- Диагонали при пересечении не образуют угол в 90 градусов.
- Диагонали не являются биссектрисами углов больших треугольников, полученных при пересечении.
- Окружность можно только описать, а не вписать.
Если для искомой фигуры применим хотя бы один из признаков, то ее возможно классифицировать как прямоугольник.
После успешной идентификации необходимо перейти к рассмотрению свойств, которые рекомендовано специалистами использовать при расчетах параметров и доказательстве утверждений (тождеств и теорем).
Важные свойства
Свойства — набор или список утверждений и тождеств, используемых при вычислениях требуемых величин, а также для доказательства теорем, а именно:
- Все углы прямые, а их алгебраическая сумма равна 360.
 1/2), т. е. квадратичное значение диагонали равно сумме сторон, каждая из которых умножена на эквивалентное значение.
1/2), т. е. квадратичное значение диагонали равно сумме сторон, каждая из которых умножена на эквивалентное значение. - Подобность малого и большого треугольников, образованных диагоналями.
- Существует только описанная окружность, диаметр которой эквивалентен диагонали прямоугольника.
- При проведении диагонали образуются два равных треугольника, являющиеся прямоугольными.
Следует отметить, что вышеописанные свойства – это требуемый минимум, которого недостаточно для выполнения вычислений и доказательства других тождеств.
Формулы и соотношения
Чтобы ориентироваться в формулах, нужно ввести некоторые обозначения.
- Диагональ – m.
- Стороны – k и l.
- Периметр – P.
- Полупериметр – р.
- Площадь – S.
- Острый угол, который образуют две диагонали – Z, а тупой – Y.
 2-14l+48=0.
2-14l+48=0. - Вычислить его корни: l1=6 и l2=8.
- Подставить в четвертый пункт и посчитать стороны: l=6 и к=8.
Следует отметить, что расчет корней производится подстановкой, при которой возникают дубли решений. Среди них требуется выбрать любых две пары. Исходя из девятого пункта, можно рассчитать значение площади, зная две стороны. Используя формулы, можно находить и другие параметры. Например, высчитать значение острого угла.
Таким образом, перед решением задач по геометрии математики рекомендуют правильно идентифицировать геометрическую фигуру при помощи признаков, а затем использовать какие-либо соотношения.
Не успеваете написать работу?
Заполните форму и узнайте стоимость
Вид работыПоиск информацииДипломнаяВКРМагистерскаяРефератОтчет по практикеВопросыКурсовая теорияКурсовая практикаДругоеКонтрольная работаРезюмеБизнес-планДиплом MBAЭссеЗащитная речьДиссертацияТестыЗадачиДиплом техническийПлан к дипломуКонцепция к дипломуПакет для защитыСтатьиЧасть дипломаМагистерская диссертацияКандидатская диссертацияКонтактные данные – строго конфиденциальны!
Указывайте телефон без ошибок! – потребуется для входа в личный кабинет.
* Нажимая на кнопку, вы даёте согласие на обработку персональных данных и соглашаетесь с политикой конфиденциальности
Подтверждение
Ваша заявка принята.
Ей присвоен номер 0000.
Просьба при ответах не изменять тему письма и присвоенный заявке номер.
Ошибка оформления заказа
Кажется вы неправильно указали свой EMAIL, без которого мы не сможем ответить вам.
Пожалуйста проверте заполнение формы и при необходимости скорректируйте данные.
Прямоугольник. Формулы и свойства прямоугольника
Навигация по странице: Определение прямоугольника Основные свойства прямоугольника Стороны прямоугольника (длина и ширина прямоугольника) Диагональ прямоугольника Периметр прямоугольника Площадь прямоугольника Окружность описанная вокруг прямоугольника Угол между стороной и диагональю прямоугольника Угол между диагоналями прямоугольника
Определение.
Прямоугольник – это четырехугольник у которого две противоположные стороны равны и все четыре угла одинаковы.
Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.Длинную сторону прямоугольника называют длиной прямоугольника, а короткую – шириной прямоугольника.
Стороны прямоугольника одновременно является его высотами.
| Рис.1 | Рис.2 |
Основные свойства прямоугольника
Прямоугольником могут быть параллелограмм, квадрат или ромб.
1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:
AB = CD, BC = AD
2. Противоположные стороны прямоугольника параллельны:
AB||CD, BC||AD
3. Прилегающие стороны прямоугольника всегда перпендикулярны:
Прилегающие стороны прямоугольника всегда перпендикулярны:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
4. Все четыре угла прямоугольника прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
5. Сумма углов прямоугольника равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника имеют одинаковой длины:
AC = BD
7. Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:
2d2 = 2a2 + 2b2
8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.
9. Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:
| AO = BO = CO = DO = | d | ||
| 2 |
10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
11. Диагональ прямоугольника является диаметром описанной окружности
12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:
∠ABC + ∠CDA = 180° ∠BCD + ∠DAB = 180°
13. В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы противоположных сторон не равны между собой (вписать окружность можно только в частный случай прямоугольника – квадрат).
Стороны прямоугольника
Определение.
Длиной прямоугольника называют длину более длинной пары его сторон. Шириной прямоугольника называют длину более короткой пары его сторон.
Формулы определения длин сторон прямоугольника
1. Формула стороны прямоугольника (длины и ширины прямоугольника) через диагональ и другую сторону:
a = √d2
b = √d2 – a2
2. Формула стороны прямоугольника (длины и ширины прямоугольника) через площадь и другую сторону:
Формула стороны прямоугольника (длины и ширины прямоугольника) через площадь и другую сторону:
| a = | S |
| b |
| b = | S |
| a |
3. Формула стороны прямоугольника (длины и ширины прямоугольника) через периметр и другую сторону:
| a = | P – 2b |
| 2 |
| b = | P – 2a |
| 2 |
4. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол α:
a = d sinα
b = d cosα
5. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол β:
| a = d sin | β |
| 2 |
| b = d cos | β |
| 2 |
Диагональ прямоугольника
Определение.
Диагональю прямоугольника называется любой отрезок соединяющий две вершины противоположных углов прямоугольника.
Формулы определения длины диагонали прямоугольника
1. Формула диагонали прямоугольника через две стороны прямоугольника (через теорему Пифагора):
d = √a2 + b2
2. Формула диагонали прямоугольника через площадь и любую сторону:
| d = | √S2 + a4 | = | √S2 + b4 |
| a | b |
3. Формула диагонали прямоугольника через периметр и любую сторону:
| d = | √P2 – 4Pa + 8a2 | = | √P2 – 4Pb + 8b2 |
| 2 | 2 |
d = 2R
5. Формула диагонали прямоугольника через диаметр описанной окружности:
Формула диагонали прямоугольника через диаметр описанной окружности:
d = Dо
6. Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
| d = | a |
| sin α |
7. Формула диагонали прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
| d = | b |
| cos α |
8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника
d = √2S : sin β
Периметр прямоугольника
Определение.
Периметром прямоугольника называется сумма длин всех сторон прямоугольника.
Формулы определения длины периметру прямоугольника
1. Формула периметру прямоугольника через две стороны прямоугольника:
Формула периметру прямоугольника через две стороны прямоугольника:
P = 2a + 2b
P = 2(a + b)
2. Формула периметру прямоугольника через площадь и любую сторону:
| P = | 2S + 2a2 | = | 2S + 2b2 |
| a | b |
3. Формула периметру прямоугольника через диагональ и любую сторону:
P = 2(a + √d2 – a2) = 2(b + √d2 – b2)
4. Формула периметру прямоугольника через радиус описанной окружности и любую сторону:
P = 2(a + √4R2 – a2) = 2(b + √4R2 – b2)
5. Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:
P = 2(a + √Do2 – a2) = 2(b + √Do2 – b2)
Площадь прямоугольника
Определение.
Площадью прямоугольника называется пространство ограниченный сторонами прямоугольника, то есть в пределах периметра прямоугольника.
Формулы определения площади прямоугольника
1. Формула площади прямоугольника через две стороны:
S = a · b
2. Формула площади прямоугольника через периметр и любую сторону:
| S = | Pa – 2a2 | = | Pb – 2b2 |
| 2 | 2 |
3. Формула площади прямоугольника через диагональ и любую сторону:
S = a√d2 – a2 = b√d2 – b2
4. Формула площади прямоугольника через диагональ и синус острого угла между диагоналями:
| S = | d2 · sin β |
| 2 |
5. Формула площади прямоугольника через радиус описанной окружности и любую сторону:
Формула площади прямоугольника через радиус описанной окружности и любую сторону:
S = a√4R2 – a2 = b√4R2 – b2
6. Формула площади прямоугольника через диаметр описанной окружности и любую сторону:
S = a√Do2 – a2 = b√Do2 – b2
Окружность описанная вокруг прямоугольника
Определение.
Окружностью описанной вокруг прямоугольника называется круг проходящий через четыре вершины прямоугольника, центр которого лежит на пересечении диагоналей прямоугольника.
Формулы определения радиуса окружности описанной вокруг прямоугольника
1. Формула радиуса окружности описанной вокруг прямоугольника через две стороны:
| R = | √a2 + b2 |
| 2 |
2. Формула радиуса окружности описанной вокруг прямоугольника через периметр квадрата и любую сторону:
| R = | √P2 – 4Pa + 8a2 | = | √P2 – 4Pb + 8b2 |
| 4 | 4 |
3. Формула радиуса окружности описанной вокруг прямоугольника через площадь квадрата:
Формула радиуса окружности описанной вокруг прямоугольника через площадь квадрата:
| R = | √S2 + a4 | = | √S2 + b4 |
| 2a | 2b |
4. Формула радиуса окружности описанной вокруг прямоугольника через диагональ квадрата:
| R = | d |
| 2 |
5. Формула радиуса окружности описанной вокруг прямоугольника через диаметр описанной окружности:
| R = | Dо |
| 2 |
6. Формула радиуса окружности описанной вокруг прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
| R = | a |
| 2sin α |
7. Формула радиуса окружности описанной вокруг прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
| R = | b |
| 2cos α |
8. Формула радиуса окружности описанной вокруг прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:
Формула радиуса окружности описанной вокруг прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:
| R = | √2S : sin β |
| 2 |
Угол между стороной и диагональю прямоугольника
Формулы определения угла между стороной и диагональю
1. Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:
| sin α = | a |
| d |
| cos α = | b |
| d |
2. Формула определения угла между стороной и диагональю прямоугольника через угол между диагоналями:
| α = | β |
| 2 |
Угол между диагоналями прямоугольника
Формулы определения угла между диагоналями прямоугольника
1. Формула определения угла между диагоналями прямоугольника через угол между стороной и диагональю:
Формула определения угла между диагоналями прямоугольника через угол между стороной и диагональю:
β = 2α
2. Формула определения угла между диагоналями прямоугольника через площадь и диагональ:
| sin β = | 2S |
| d2 |
Все таблицы и формулы
Как найти диагональ прямоугольника — mathsathome.com
Как найти диагональ прямоугольника Видеоурок:
Как найти диагональ прямоугольника с помощью теоремы Пифагора
Чтобы найти диагональ прямоугольника с помощью теоремы Пифагора, используйте формулу d = √(l² + w²), где l — длина, а w — ширина прямоугольника. Например, диагональ прямоугольника длиной 4 см и шириной 3 см равна d = √(4² + 3²). Оценивая это, d = √ 25 и, следовательно, длина диагонали 5 см.
Диагонали прямоугольника равны по длине и делят прямоугольник на два равных треугольника. Это означает, что прямоугольник разделен на два прямоугольных треугольника, из которых можно использовать теорему Пифагора. этот. Диагональ – это гипотенуза треугольника, образованного делением прямоугольника на две части.
Это означает, что прямоугольник разделен на два прямоугольных треугольника, из которых можно использовать теорему Пифагора. этот. Диагональ – это гипотенуза треугольника, образованного делением прямоугольника на две части.
Формула для нахождения диагонали прямоугольника
Формула для нахождения диагонали прямоугольника: d = √(l² + w²), где l — длина, а w — ширина прямоугольника. Например, диагональ прямоугольника длиной 6 м и шириной 2 м определяется как d = √(6² + 2²). Оценивая это, d = √40 и, следовательно, длина диагонали составляет примерно 6,32 м.
Формула длины диагонали прямоугольника
Пример 1:
Прямоугольник имеет длину 6 м и ширину 2 м.
Поэтому и .
Подставляя эти значения в формулу, получаем .
Это становится и оценивая это, диагональ составляет примерно 6,32 м в длину.
Пример 2:
Диагональ какого прямоугольника наибольшая?
Первый прямоугольник имеет длину 8 см и ширину 4 см.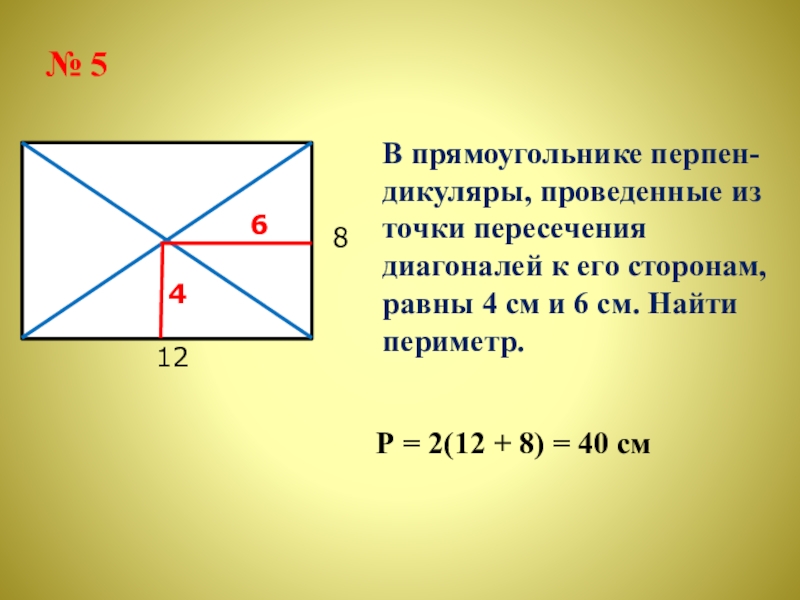
, что равно . Оценивая это, диагональ составляет примерно 8,94 см в длину.
Второй прямоугольник имеет длину 7 см и ширину 5 см.
, что равно . Исходя из этого, длина диагонали составляет примерно 8,60 см.
Следовательно, у первого прямоугольника наибольшая диагональ.
Калькулятор диагонали прямоугольника
Калькулятор диагонали прямоугольника рассчитает длину диагонали прямоугольника, если известны длина и ширина прямоугольника.
Просто введите длину и ширину прямоугольника в калькулятор, чтобы рассчитать длину диагонали.
Как найти диагональ квадрата
Чтобы найти длину диагонали квадрата, используйте формулу d=√2×a, где a — длина стороны квадрата. Например, длина диагонали квадрата длиной 10 см равна d=√2× 10. Таким образом, длина диагонали равна 14,1 см.
Формула длины диагонали квадрата с длинами сторон «а»
Формула длины диагонали квадрата выводится из теоремы Пифагора для длины диагонали прямоугольника.
Для прямоугольника длина диагонали определяется как , где l — длина, а w — ширина прямоугольника.
Для квадрата длина и ширина равны. Если длина и ширина равны «а», то становится .
Это упрощается до .
Это можно записать как , что равно
Как найти диагональ прямоугольника, зная площадь
Если площадь и одна сторона прямоугольника известны, разделите площадь на известную сторону, чтобы найти другую сторону . Этими двумя сторонами являются длина (l) и ширина (w). Затем используйте теорему Пифагора, d = √(l² + w²) , чтобы вычислить диагональ прямоугольника.
Пример 1:
Например, найдите диагональ прямоугольника площадью 20 м 2 и длиной 10 м.
Сначала разделите площадь на длину, чтобы найти ширину.
и так, ширина 2м.
Теперь мы можем использовать для нахождения диагонали, учитывая, что l=10 и w=2.
, который становится , что равно 10,2 м.
Пример 2:
Найдите площадь прямоугольника, если длина диагонали 5 см, а длина 4 см.
Чтобы найти площадь прямоугольника, используйте формулу .
Find Нам нужно найти высоту по теореме Пифагора.
Чтобы найти ширину, зная диагональ, воспользуйтесь формулой .
Поскольку диагональ равна 5 см, а длина 4 см, получается , что равно .
Ширина 3 см. Это высота прямоугольника.
.
Как найти диагональ прямоугольника по периметру
Если периметр и длина стороны прямоугольника известны, вычтите известную длину стороны из половины периметра, чтобы найти длину другой стороны. Эти две стороны — длина (l) и ширина (w). Затем используйте теорему Пифагора, d = √(l² + w²) , чтобы вычислить диагональ прямоугольника.
Пример 1:
Найдите диагональ прямоугольника с периметром 26 см и длиной 7 см.
Сначала найдите ширину прямоугольника, вычитая длину из половины периметра.
Половина периметра 13 см. 13 – 7 = 6, значит, ширина прямоугольника 6 см.
Теперь, когда длина = 7, а ширина = 6, становится .
Это равно и, следовательно, длина диагонали составляет примерно 9,22 см.
Как найти длину диагонали ромба?
Ромб также известен как четырехугольник с четырьмя сторонами. Считается частным случаем параллелограмма. Ромб имеет параллельные противоположные стороны и равные противоположные углы. Ромб также известен под названием алмаз или ромбовидный алмаз. У ромба все стороны ромба равны по длине. Кроме того, диагонали ромба пересекаются пополам под прямым углом.
Свойства ромба
Ромб обладает следующими свойствами:
- У ромба все стороны равны.
- Диагонали ромба делят друг друга пополам под прямым углом.
- Противоположные стороны ромба по своей природе параллельны.
- Сумма двух смежных углов ромба равна 180 o .
- В ромбе нет вписанной окружности.

- Вокруг ромба нет описанной окружности.
- Диагонали ромба образуют четыре прямоугольных треугольника.
- Эти треугольники конгруэнтны друг другу.
- Противоположные углы ромба равны.
- При соединении середины сторон ромба образуется прямоугольник.
- При соединении середины половины диагонали образуется еще один ромб.
У ромба четыре ребра соединены вершинами. При соединении противоположных вершин ромба образуются дополнительные ребра, в результате чего образуются диагонали ромба. Следовательно, ромб может иметь две диагонали, каждая из которых пересекается под углом 90°.
Свойства диагонали ромба
Диагонали ромба обладают следующими свойствами:
- Диагонали делят друг друга пополам под прямым углом.
- Диагонали ромба делятся на четыре равных прямоугольных треугольника.
- Диагонали ромба могут быть или не быть равными по длине.

Длину диагоналей ромба можно рассчитать, используя следующие методы:
По теореме Пифагора
Примем d 1 за диагональ ромба.
Поскольку, как мы знаем, все смежные стороны ромба образуют угол 90 градусов.
Следовательно,
В треугольнике BCD имеем
BC 2 + CD 2 = BD 2
Теперь имеем
В случае квадратного ромба со всеми сторонами равными ,
Квадрат Диагональ: a√2
где а длина стороны квадрата
В случае прямоугольного ромба имеем 05 2 ]
где
- l — длина прямоугольника.
- b — ширина прямоугольника.
Используя площадь ромба
Рассмотрим O как точку пересечения двух диагоналей, а именно d 1 и д 2 .
Теперь,
Площадь ромба эквивалентна,
A = 4 × площадь ∆AOB
= 4 × (½) × AO × OB кв. единиц
= 4 × (½) × ( ½) d 1 × (½) d 2 квадратных единиц
= 4 × (1/8) d 1 × d 2 квадратных единиц
= ½ × d 90 225 1 × д 2
Следовательно, Площадь ромба = A = ½ × d 1 × d 2
Площадь ромба по диагоналям
Рассмотрим ромб ABCD, имеющий две диагонали, т. е. AC и BD.
- Шаг 1: Вычислите длину отрезка AC, соединив точки A и C. Пусть это будет диагональ 1, т.е. d 1 .
Диагонали ромба перпендикулярны друг другу и стягивают прямоугольные треугольники при пересечении друг с другом в центре ромба.
- Шаг 2: Аналогичным образом вычислите длину диагонали 2, т.
 е. d 2 , которая является расстоянием между точками B и D.
е. d 2 , которая является расстоянием между точками B и D. - Шаг 3: Умножьте обе вычисленные диагонали, д 1 и д 2 .
- Шаг 4: Результат получается делением произведения на 2.
Результат даст площадь ромба ABCD.
Примеры вопросов
Вопрос 1. Одна из сторон ромба равна 5 см. Одна из диагоналей ромба равна 8 см, вычислите длину другой диагонали.
Решение:
Предположим, что ABCD — ромб, где AC и BD — диагонали.
Имеем,
Сторона ромба равна 5 см
BD = 8 см
Так как, мы знаем, что диагонали ромба перпендикулярно делят друг друга пополам.
∴ BO = 4см
По теореме Пифагора имеем,
В прямоугольном △AOB,
⇒ (AB) 2 = (AO) 2 + (БО) 2
⇒ (5) 2 = (AO) 2 + (4) 2
⇒ 25 = (AO) 2 + 16
⇒ (AO) 2 = 9
∴ AO = 3 см
⇒ AC = 2 × 3 = 6 см
∴ Длина другой диагонали ромба эквивалентна 6 см.
Вопрос 2. Вычислите площадь ромба с диагоналями, равными 6 см и 8 см соответственно.
Решение:
Знаем,
Диагональ 1, d 1 = 6 см
Диагональ 2, d 2 = 8 см
Площадь ромба, А = (d 1 × d 2 ) / 2
Подставляя значения,
= (6 × 8) / 2
= 48 / 2
= 24 см 2
Следовательно, площадь ромба равна 24 см 2 .
Вопрос 3. Прямоугольный парк имеет длину 10м и ширину 8м. Вычислите диагональ парка.
Решение:
Имеем,
Длина = 100м
Ширина = 8 мВычисление диагоналей, получаем,
9000 6 Диагональ прямоугольника = √[l 2 + b 2 ]= √[10 2 + 8 2 ]
= √[164]
= 12,80 м
Вопрос 4.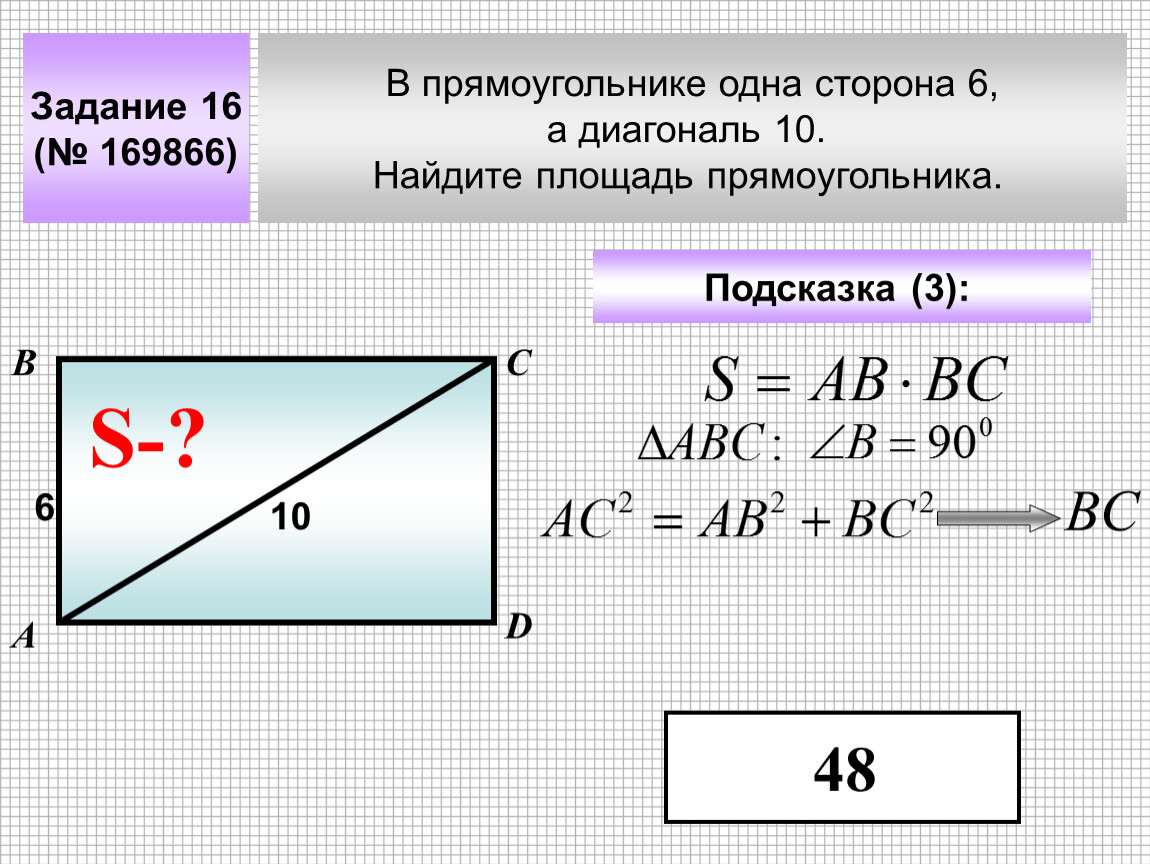

 1/2), т. е. квадратичное значение диагонали равно сумме сторон, каждая из которых умножена на эквивалентное значение.
1/2), т. е. квадратичное значение диагонали равно сумме сторон, каждая из которых умножена на эквивалентное значение. 2-14l+48=0.
2-14l+48=0.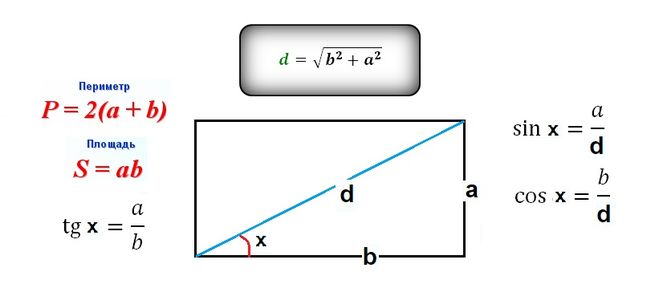

 е. d 2 , которая является расстоянием между точками B и D.
е. d 2 , которая является расстоянием между точками B и D.