Парабола в архитектуре: Парабола в архитектуре – математика, презентации – asnka.ru – КСМ

Содержание

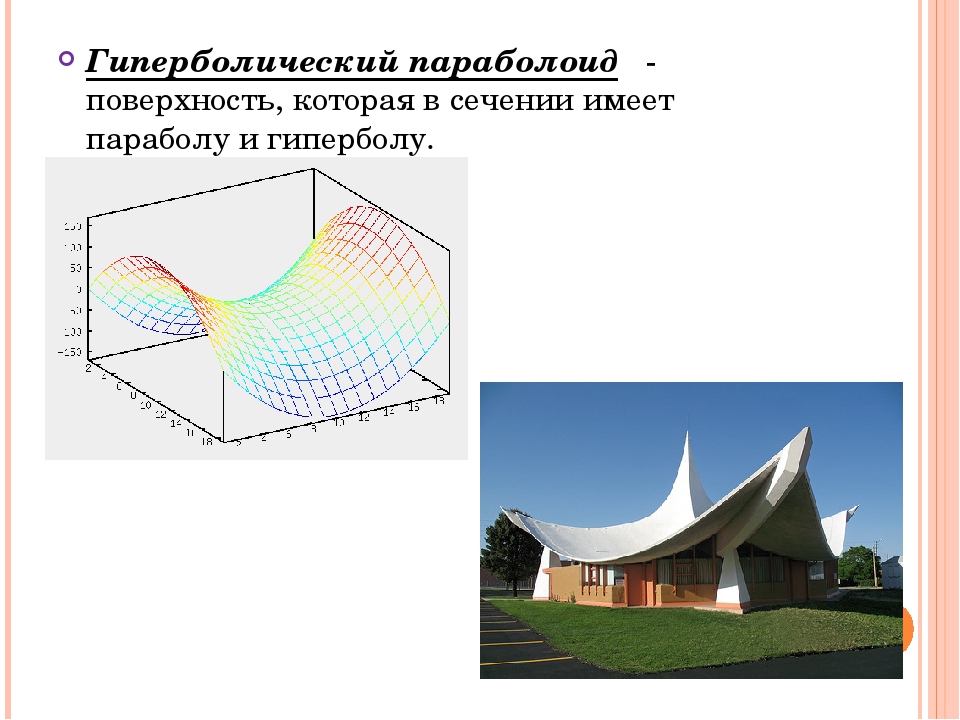
Парабола в архитектуре – математика, презентации

В современном понимании архитектура — это искусство проектировать и строить здания, сооружения и их комплексы. Сложность этого процесса заключается в необходимости создания архитектурных объектов, которые сочетают в себе гармоничные архитектурные решения с высоким качеством строительства и функциональностью предлагаемых помещений. Для того, чтобы предусмотреть каждый из этих аспектов, архитекторы с древних времен обращались к математике, именно она позволила им создать великие сооружения, которые, благодаря своей устойчивости и надежности, сохранились до наших дней. Примерами таких зданий являются: Храм Василия Блаженного, Храм Парфенон, созданные с использованием золотого сечения; Казанский собор, гостиница Прибалтийская, Загородная резиденция Петра Великого в Петергофе, в основе которых лежит принцип симметрии и другие.

Парабола (греч.

παραβολ? — приложение) — кривая, точки которой одинаково удалены от некоторой точки, называемой фокусом, и от некоторой прямой, называемой директрисой параболы.
Парабола с вершиной в начале координат является графиком функции y=kx2 при k ≠ 0, ось y является осью параболы, ветви параболы направлены вверх при k>0 и вниз при k<0.
В архитектуре чаще встречаются сооружения и конструкции, в основе которых лежит парабола, оси которой направлены вниз. Это не случайно именно такая ее форма сочетает в себе геометрическую красоту и механическую приспособленность к напряжениям и деформациям, вызываемым весом сооружений, именно это ее свойство привлекало и сейчас привлекает архитекторов использовать данную функцию при строительстве мостов и различный арок.

Рассматривая подробнее функцию y=kx2 при k<0, отметим, что область определения этой непрерывной функции — (-∞, +∞),y наиб.

=0 (достигается при x=0), y наим. не существует. Именно это свойство позволяет использовать функцию параболы для создания сооружений любой высоты.

Симметричность же данной функции относительно оси абсцисс позволяет достигать равномерного распределения нагрузки, что способствует устойчивости и прочности сооружений, в основе которых так или иначе лежит парабола.
Стоит отметить, что парабола является узнаваемым элементом архитектуры настоящего и прошлого.

В применении параболической дуги при постройке мостов и кровельных перекрытий можно различать не менее четырех различных типов. Первый тип представляют висячие (цепные) мосты с тросами, провисающими по кривой параболической формы. Ко второму типу относим тот случай, когда вершина параболической арки находится под проезжей частью. У мостов третьего типа параболическая арка пересекает проезжую часть. Наконец, сооружения, у которых параболическая арка целиком расположена над путем, как в случае перекрытий, принадлежат к четвертому типу.

Филиал Казанского (Приволжского) федерального университета в г. Елабуга . Крестовоздвиженская церковь Казанско-Богородицкого монастыря в г. Казань. Купола этих архитектурных сооружений являются конструкциями параболической формы. Плавность и в тоже время четкость изгибов параболической функции, лежащей в основе куполов позволяет им гармонично вписываться во внешний облик здания, не утяжеляя его.

Как было сказано ранее именно в конструкциях арок и мостов параболическая форма встречается чаще всего.Арка влюбленных в Парке Черное озеро в г. Казань. Благодаря особенностям конструкции арка обладает удивительным акустическим эффектом. Двое влюбленных, находящихся по разные стороны арки, могут шепотом признаваться друг другу в любви, и каждое слово будет услышано любимым человеком.

Мензелинский мост в г. Мензелинск.

Лебедевский (Горбатый) Мост, г. Казань.
Применение параболической формы нашло применение и в будущих проектах архитектурных сооружений Республики Татарстан, примером такого проекта является здание Национальной библиотеки в г. Казань.
Подводя итог вышесказанному, хочется еще раз сделать акцент на уникальности параболической формы, которая способна придавать изящество и красоту сооружениям, обеспечивая при этом надежность и прочность конструкций.

Просмотр содержимого документа
«Парабола в архитектуре»

Параболы в арочных мостах | Обучонок

В процессе работы над индивидуальным исследовательским проектом по математике на тему “Параболы в арочных мостах” автором была поставлена цель, изучить материал о свойствах квадратичной функции и ее графика – параболы, исследовать графики квадратичной функции в арочных мостах Санкт-Петербурга.

Подробнее о работе:

В ученической исследовательской работе по математике “Параболы в арочных мостах” автором было дано определение понятие “парабола” и приведены сведения из истории мостостроения в России с XII по XIX века. В работе подробно описываются виды мостов, автор останавливается на изучении принципа строительства мостов арочного вида.

Учебная исследовательская работа по математике на тему “Параболы в арочных мостах” будет интересна учащимся 9 класса, рассматривает теоретическую базу о построении арочных мостов с применением принципа параболы. В работе исследуется парабола в мостостроении, проводится анализ построения Санкт-Петербургских арочных мостов: Казанского, Синего, Троицкого, моста в Юсуповском саду и Арки-галереи над Зимней канавкой.

В исследовательском проекте по математике представлена теория квадратичной функции и ее графика, найдены арочные мосты в Петербурге и представлены их фотографии. На фотографиях арочных мостов города Санкт-Петербурга автор схематично изобразил параболу, расположенную на оси координат, и произвел вычисление уравнений графиков квадратичной функции, изучил их свойства.

1.3. Виды мостов.
1.4. Арочные мосты.
2. Парабола в мостостроении.
2.1. Казанский мост.
2.2. Арка-галерея над Зимней канавкой.
2.3. Мост в Юсуповском саду.
2.4. Синий мост.
2.5. Троицкий мост.
Заключение
Используемая литература
Приложения

Введение

Ни одного архитектурного сооружения в нашем мире не существовало бы без предварительных точных расчетов, которые помогает делать наука под названием математика. В повседневной жизни довольно часто нам встречаются дугообразные конструкции; эта форма широко распространена не только из-за эстетичного внешнего вида, но и из-за способности выдерживать нагрузки, вызываемые весом самого сооружения и дополнительными факторами (сейсмическая активность в регионе, транспорт и т.д.). К таким сооружениям относятся арки, купола храмов, акведуки, однако в этой работе будут рассмотрены мосты Санкт-Петербурга.

Цели работы:

Изучить материал о свойствах квадратичной функции и ее графика- параболы.
Исследовать графики квадратичной функции в арочных мостах Санкт-Петербурга.

Для достижения цели я поставила следующие задачи:

Изучить литературу про мосты Санкт-Петербурга.
Изучить теорию квадратичной функции и ее графика.
Найти арочные мосты в Петербурге.
Сфотографировать эти мосты.
Овладеть методикой задания уравнениями графиков квадратичной функции и исследовать их свойства.

Объект исследования: арочные мосты Санкт-Петербурга

Предмет исследования: свойства параболы, применяемые при строительстве арочных мостов Санкт-Петербурга

Продукт научно-исследовательской работы: презентация, включающая фотографии мостов Санкт-Петербурга, сделанные автором.

Парабола

Термин функция (от лат. function – исполнение, совершение) впервые был введен немецким ученым Г.

Лейбницем в конце 17 века. Функцией называется зависимость между двумя переменными x и y, при которой каждому значению х соответствует единственное значение у. Одним из способов задания функции является график. Графиком функции называется множество точек в системе координат, абсциссы которых равны аргументу, а ординаты – соответствующим значениям функции.

Существует довольно много видов функций: линейная, квадратичная, степенная, показательная, логарифмическая, тригонометрическая и другие, каждая из них задается уравнением и графиком. Линейная функция задается прямой, квадратичная – квадратичной параболой, степенная функции вида у=х2k+1 (где k – натуральное число) – кубической парабола, функция вида y – гиперболой и тд. В данной работе будут рассмотрены исключительно квадратичная функция и ее график.

Функция вида y=ax2+bx+c, где a, называется квадратичной. Графиком этой функции является парабола. Парабола – это геометрическое место точек, равноудаленных от данной прямой и данной точки.

Рис. 1. График квадратичной функции

Чтобы построить график функции вида y=ax2+bx+c, нужно найти координаты вершины графика.

Х вершины = (-b)/2a; для нахождения у вершины нужно подставить значение найденного x в данное уравнение;

график функции y=ax2+bx+c получается из графика функции у=aх2 сдвигом в точку (х вершины; у вершины).

Довольно часто мы сталкиваемся с параболическими формами. Например, во время или после дождя мы наблюдаем радугу. В лепестках некоторых цветов, в очертании горных хребтов и вершин можно разглядеть параболу.

Парабола в колокольчике

Гуляя по городу, мы часто видим дугообразные конструкции. Архитекторы используют параболическую форму в проектировании арок, мостов, куполов, потолков. Во-первых, именно такая форма придает эстетичный вид, во-вторых, параболическим конструкциям присуща прочность, потому что сила, создаваемая нагрузкой на мост или арку, не толкает вниз, а распределяется вдоль дуги, то есть эти строения поддерживают сами себя.

В куполах всех храмов и церквей используется этот же принцип. В данной работе будут рассмотрены мосты в Санкт-Петербурге.

Прежде чем рассматривать виды мостов и их преимущества, познакомимся с историей мостостроения в России.

Из истории мостостроения в России с XII по XIX века

Постройка мостов, вероятно, началась очень давно. При Владимире Мономахе в 1115 году был построен наплавной мост через Днепр в Киев, при Дмитрии Донском во время осады Твери были построены 2 моста, а во время войны с татарами в 1380 году возвели мост через Дон. Кроме того, в Новгородской летописи упоминается о «разборчатых» мостах в Новгороде через реку Волхов(рис.4).

Рис.4. Мост 12 века через реку Волхов

Наплавные мосты состояли из закрепленных между собой плотов и лодок. Именно наплавные мосты были наиболее распространены в России в этот период из-за простоты и дешевизны конструкции.

Возводной мост, прилегавший к городской стене, делался подъемным. Первое указание относительно употребления таких мостов относится к 1229 году. Механизм, приводивший мост в движение, состоял из коромысла, который вращался между столбами, и цепей.

Первый каменный мост начали строить в 1643 году при Михаиле Федоровиче Романове, однако в связи со смертью царя в 1645 году строительство было остановлено. Только в 1687 году первый каменный мост был открыт.

С воцарением Петра Великого инженерное искусство развивалось неимоверно быстро, но при царе мостов не строилось. Петр I воспринимал Петербург как крупнейший порт, куда прибывали суды всех стран Европы, а мосты мешали судоходству. Также в городе на Неве ежегодно случались наводнения и штормовые бури, которые могли повредить конструкции. Но все же Петр I сделал исключение, издав приказ о строении деревянного моста, соединявшего Березовый и Заячий острова, с целью транспортировки грузов к Петропавловской крепости.

В царствование Екатерины I в 1727 году был возведен первый наплавной мост через Неву. При Анне Иоанновне возвели несколько каменных мостов на сваях, например, Симеоновский через Фонтанку, оформленный под каменный арочный мост. Остальные мосты через Мойку и Фонтанку построены в период времени 1742-1749гг., т.е. во время правления Елизаветы Петровны. При ней же был возведен Исаакиевский мост(рис.4).

При Екатерине II в Петербурге началась замена деревянных мостов на каменные на реке Фонтанке, строение Казанского и Каменного мостов через Екатерининский канал[2], в Москве через реку Яузу был возведен Дворцовый мост. С началом строительства в 1817 году Петербурго-Московского шоссе появилось множество каменных мостов, пролеты которых могли достигать 9 саж[3]. В 40-х годах строилось несколько каменных мостов в Тифлисе[4], например, Михайловский мост с пролетом в 15 саж (32м).

Чугунные арочные мосты впервые появились в 1806 году в Петербурге при Александре I, это были первые металлические мосты в России. Были построены Полицейский, Красный, Синий, Поцелуев, Мало-Семеновский мосты.

Цепные мосты введены в Россию в 1822 году по предложению французских инженеров. Распространение таких мостов захватило период с 1824 по 1853 год. К цепным мостам относятся Пантелеймоновский, пешеходные через Екатерининский канал и Мойку, Египетский, проволочный Лиговский через Западный Бур в Брест, мост через Нарву в Ивангород, Киевский через Днепр и Островский через реку Великую.

До 1873 года из подвижных мостов с постоянными опорами применялись только подъемные с горизонтальной осью вращения. Поворотные мосты появились в первые в 1850 году при строительстве Николаевского моста в Петербурге и цепного моста в Киеве в 1853 году.

Виды мостов

I. Балочный мост

Балочные мосты используются для перекрытия небольших пролетов. Отличаются простотой строения и прочностью. Балочные мосты способны выдержать большие вертикальные нагрузки, но не горизонтальные, такие как сильный ветер. Также такие мосты чувствительны к деформации основания. Из-за этих недостатков балочные конструкции почти не используются в современном мостостроении.

Рис.5. Бердов мост

II. Висячий мост

Главное преимущество висячих мостов состоит в том, что основной пролет можно сделать максимально длинным, используя небольшое количество материала. Балочные мосты не требуют дополнительных опор, также их можно строить достаточно высоко, что дает возможность судам проходить под ними. Но под действием сильного ветра опоры крайне неустойчивы, поэтому во время штормов некоторые мосты перекрывают.

Рис.6. Почтамтский мост

III. Вантовый мост

Это тип висячего моста. Имеет такие же преимущества, но по сравнению с висячим он более устойчив к суровым погодным условиям.

Рис.7. Большой Обуховский мост

Арочные мосты

Арочный мост – мост с пролётными строениями, основными несущим конструкциями которых служат арки. [5]

Основные размеры элементов арочных мостов – высота и ширина балок, толщина плиты, высота и ширина арок, количество арматуры и т.п. – окончательно устанавливаются на основании расчета сооружения в соответствии с действующими на сооружение нагрузками и качеством материалов, из которых строится мост.

Выбор толщины арки затруднителен вследствие большого разнообразия факторов, влияющих на этот выбор, таких как величина нагрузки, марка бетона и т.д. Примерно можно принимать:

d= 145÷150L;

где d – толщина арки, L – расчетный пролет арки.[6]

Рис.8. Размеры модели моста

Также для строения моста необходимо рассчитать максимально возможную нагрузку на конструкцию. Для этого используется формула Журавского, которая представлена на рис.9.

Рис.9. Формула Журавского

Казанский мост

Казанский мост перекинут через канал Грибоедова, соединяя Казанский и Спасский острова. Длина переправы — 17,35 метров, ширина — 95 метров.

Это третий по ширине мост в Петербурге после Синего и Аптекарского мостов.

С 1716 года существовал деревянный мост через речку Кривушу. В 1737 году мост получил имя Рождественский, поскольку рядом располагалась церковь Рождества Богородицы. Со второй половины XVIII века Рождественскую церковь стали называть Казанской. Такое же наименование закрепилось и за новым каменным мостом, построенным в 1766 году.

В 1805-1806 годах, в связи с постройкой Казанского собора и перепланировкой участка, примыкающего к Невскому проспекту, мост перестроили, предположительно, по проекту архитектора Л.И. Руска. Мост расширили до 95 м, а его длина составила 17,5м.

На фотографии Казанского моста (см. Приложение 1) представлены система координат и график квадратичной функции. Чтобы задать уравнение, мною был введен единичный отрезок.

y=ax²+bx+c

Арка-галерея над Зимней канавкой

Арка-галерея перекинута через Зимнюю канавку. Арка была построена при Екатерине II, в 1780 году, для соединения Большого Эрмитажа с Эрмитажным театром. Работы были выполнены по проекту архитектора Ю.М. Фельтена. Существует легенда, что завистники Фельтена пустили слух о непрочности конструкции арки, но Екатерина Алексеевна, дабы развеять сомнения, устроила грандиозный пир со множеством приглашенных. Арка не деформировалась под огромным грузом, и все слухи прекратились.

На фотографии арки-галереи (см. Приложение 2) также представлены система координат и график квадратичной функции.

y=ax²+bx+c

Мост в Юсуповском саду

В 1727 году один из свободных участков правого берега Фонтанки по приказу императора был передан во владения князя Григория Дмитриевича Юсупова. На плане города 1753 года можно было увидеть дом, обращенный к саду. Сад простирался до садовой улицы и вместе с прудом представлял собой великолепный образец английского пейзажного сада. Через пруд был перекинут мост.

Аналогично предыдущим примерам, рассмотрим скрытую в мосте параболу.

y=ax²+bx+c

Синий мост

Синий мост через реку Мойку – самый широкий в Санкт-Петербурге (99 метров), является частью Исаакиевской площади.

Берега реки Мойки начали застраивать жилыми домами уже в начале 18 века. В 1736 – 1737 годах были проведены работу по углублению реки, а берега укреплены деревянными щитами. Синий мост первоначально был подъемным, деревянным. В середине 18 века его перестроили.

В 1842 году в связи с постройкой Мариинского дворца мост значительно расширили в сторону Нового переулка (ныне переулок Антоненко). Название Синий мост идет от первоначального деревянного моста, который был выкрашен в синий цвет. Одинаковые по внешнему виду мосты в 18 веке красили в разные цвета специально для различия, чтобы они имели «свое лицо»[7]

Фотография моста представлена в Приложении 4

y = ax2+bx+с

Троицкий мост

Троицкий мост соединяет центральную часть города с Петроградской стороной. Перекинут через Большую Неву на оси Суворовской площади и Троицкой площади, от которой отходит Каменноостровский проспект.

До строительства моста на этом месте в течение ста лет наводили наплавной мост. Назывался он Петербургским, так как вел на Петербургский (ныне Петроградский) остров, затем его звали Троицким – по Троицкой площади.

Постоянный десятипролетный Троицкий мост через Неву был сооружен в 1897 – 1903 годах по проекту французской фирмы «Батильон». Руководили строительными работами русские зодчие и инженеры – Л.Н. Бенуа, Г.И. Котов, Г.Г. Кривошеин и другие.

В 1920-х годах Троицкий мост был переименован в мост Равенства. В конце 1934 года его назвали Кировским в память о Сергее Мироновиче Кирове[8]. Первоначальное имя моста возвращено в 1991 году.[9]

Как было сказано ранее, мост состоит из 10 пролетов. Мною будут рассмотрены 2 центральные арки, длины которых равны 76,4м и 96,4м (см. Приложение 5).

1) Длина арки – 76,4м

y = ax2+bx+с

Заключение

Мосты играют важную роль в архитектурном облике Петербурга. Наш город занимает первое место в стране и одно из первых мест в мире по их количеству. В Северной Венеции имеется около 500 мостов различных видов, среди них более 20 разводных.

Около 300 мостов нашего города являются арочными, поскольку именно параболическая форма придает конструкции элегантность и изящество. Помимо изысканного внешнего вида, дугообразная конфигурация способствует равномерному распределению нагрузки на мост.

Работа над проектом позволила более детально изучить свойства квадратичной функции и ее графика, а, главное, показать практическое применение этих свойств при строительстве арочных мостов в Санкт-Петербурге.

В результате данного исследования была получена методика задания уравнениями графиков квадратичной функции по фотографиям.

Мне было интересно делать данный проект, потому что он совмещает два моих любимых предмета – математику и историю. Мне удалось подробнее познакомиться с историей своего города, в частности узнать интересные факты из истории мостостроения.

И в заключении, этот материал является актуальным для сверстников, поскольку мы живем в городе, в котором мосты являются неотъемлемой частью нашей жизни.

Список используемых источников

Барсунов К.П. Расчет арочных мостов// Учебное пособие, 1956. – 118с.
Беляев Р. Как устроен мост?// Самокат, 2019. – 64с.
Бунин М.С. Мосты Ленинграда // СПб.: Стройиздат, 1986. – 280 с.
Вейнблат Б.М., Колоколов Н.М. Строительство мостов//Учебник. Второе издание.-М.: Транспорт 19Вейнблат Б.М., Колоколов Н.М. Строительство мостов//Учебник. Второе издание.
-М.: Транспорт 1984г. -504с.
Гельфанд И.М. Функции и графики//7-е издание, стереотипное.-М.:МЦНМО, 2006. – 120с.
Горбачевич К.С., Хабло Е.П. Почему так названы? // 5-е издание – СПб., «Норинт», 1998. – 352 с.
Гордеев В.Н. Нагрузки и воздействия на здания и сооружения// Справочное пособие. ИАСВ, 2007. – 477с.
Дмитриева Е.В. Санкт-Петербург: Пособие по истории города с заданиями и тестами // 4-е издание – СПб.: КОРОНА принт 2001. – 336 с.
Зинева Л.А. Справочник инженера-строителя//Феникс, Ростов–на-Дону, 2006. – 622с.
Иванов А.А. Истории и легенды старого Петербурга// Центрполиграф, 2019. – 575с.
Кукурузова Н.В. «Богаче Романовых?..» О богатстве князей Юсуповых//Юсуповский дворец (СПб ДКРП). – СПб., 2006. -128 с.
Курлянд В.Г. Строительство мостов: учебное пособие для вузов // Москва: МАДИ, 2012. – 176 с.
Лившиц Я.Д., Онищенко М.М. Примеры расчета железобетонных мостов// К.: Вища шк. Головное изд-во, 1986. – 263с.
Метальникова М.В. 500 лучших мест Санкт-Петербурга // Москва: Эксмо, 2014. – 416 с.
Николаи Л.Ф. Краткие исторические данные о развитии мостового дела в России // СПб., 1898. – 119 с.
Поляков Л.П. Расчет арочных мостов // Государственное издательство литературы по строительству и архитектуры УССР – Киев, 1962. – 180с.
Пунин А.Л. Архитектура отечественных мостов // СПб.: Стройиздат, 1982. – 152 с.
Юсупов Ф.Ф. Князь Феликс Юсупов: Мемуары в двух книгах // Москва: ЗАХАРОВ, 2018. – 432 с
Большая советская энциклопедия: [Электронный ресурс].
Официальный сайт Библиотеки физико-математической школы: [Электронный ресурс].
Мир энциклопедий: [Электронный ресурс]. URL:
Официальный сайт СПб ГБУ «Мостотрест»:[Электронный ресурс].

Приложение 1. Казанский мост

Приложение 2. Арка-галерея над Зимней канавкой

Приложение 3. Мост в Юсуповском саду

Приложение 4. Синий мост

Приложение 5. Троицкий мост

Если страница Вам понравилась, поделитесь в социальных сетях:

Гиперболы, параболы, миллиметровка и… матрешки

В полушаге от «Стерлинга» Объявлены победители RIBA National Awards за 2017 год.

Представляем все 49 сооружений-лауреатов, от гробницы Ричарда III до института сварки. Гипар дизайна Музей дизайна в Лондоне по проекту Джона Поусона – реконструкция здания Института Содружества бюро RMJM 1960-х годов. Заменить нельзя построить Лондонское бюро Allies & Morrison решило поспорить с Томасом Хезервиком и предложило для родного города альтернативный проект моста-сада. 46 претендентов на «Стерлинга» Стали известны победители RIBA National Awards за 2016 год.

Представляем все 46 зданий-лауреатов. Возвращение в доки Herzog & de Meuron представили проект круглой башни для комплекса Вуд-ворф в Лондоне. Британские награды Объявлены лауреаты региональных премий RIBA и обладатели ежегодной награды AJ100 издания The Architects’ Journal. Жилая арена В Лондоне завершена реконструкция стадиона «Хайбери» по проекту бюро «Элайз & Моррисон».

Спортивное проектирование В Лондоне утвержден проект медиа-центра Олимпиады-2012 мастерской «Элайз & Моррисон», а бюро RMJM будет заниматься не только спортивной деревней в Глазго для Игр Содружества-2014, но и всеми новыми сооружениями к Играм в Дели 2010 года. Доха: воссоздание идентичности В столице Катара планируется заново возвести исторический центр. Терракотовый фасад Власти Лондона утвердили проект Центральной школы балета бюро «Элайз & Моррисон».

Юбилейная увертюра В Бонне представлены работы участников конкурса на проект «Фестивального зала Бетховена». Городская мозаика Многоуровневый гараж по проекту «Элайз & Моррисон» открылся в Шеффилде. Очередной раунд битвы стилей Неоклассический и модернистский проекты новой гостиницы у королевского дворца Хэмптон-Корт близ Лондона представлены на рассмотрение местному муниципалитету.

Третья попытка Объявлен шорт-лист Премии Стерлинга этого года; постройка Захи Хадид вошла в этот престижный список в третий раз. Наблюдение за небесными светилами В Гринвиче открылось новое здание планетария Королевской Обсерватории. Лучшие здания Британии-2004 Объявлены лауреаты британской премии «Лучшее здание года», присуждаемой Королевским опекунским советом по делам искусств [Royal Fine Art Commission Trust].

Особенности методики преподавания темы «Парабола и параболоид» в курсах математики и инженерной графики Текст научной статьи по специальности «Строительство и архитектура»

Мурашкина Т. И., Королев Е. А., Егоров А. Ю. Особенности методики преподавания темы «Парабола и параболоид» в курсах математики и инженерной графики // Научно-методический электронный журнал «Концепт». -2017. – № V11. – 0,4 п. л. – URL: http://e-koncept.ru/2017/171045.htm.

ART 171045 УДК 378.147

Мурашкина Татьяна Ивановна,

кандидат технических наук, доцент ФГБОУ ВО «Московский государ ственный технический университет им. Н. Э. Баумана», г. Москва [email protected]

Королев Евгений Алексеевич,

студент ФГБОУ ВО «(Московский государственный технический университет

им. Н. Э. Баумана», г. Москва

[email protected]

Егоров Александр Юрьевич,

студент ФГБОУ ВО «(Московский государственный технический университет им. Н. Э. Баумана», г. Москва Sasha361 [email protected]

Особенности методики преподавания темы «Парабола и параболоид» в курсах математики и инженерной графики

Аннотация. Актуальность данной работы обусловлена особым положением линий и поверхностей второго порядка в курсах аналитической геометрии и инженерной графики в техническом университете. Парабола, а также соответствующий ей в трёхмерном мире параболоид играют важную роль во многих физических процессах. Вследствие этого они нашли широкое применение во многих инженерных, технических и других устройствах, в архитектуре и просто в повседневной жизни. В данной статье авторы рассматривают математические свойства параболы и параболоида, а также особенности их графического построения. Содержание статьи представляет интерес для студентов технических и математических специальностей, преподавателей математики и инженерной графики, а также старшеклассников, готовящихся к поступлению в вузы на специальности технического или математического направлений, поскольку перспективы развития современного школьного образования связаны с возрастанием роли его политехнических компонентов.

Ключевые слова: парабола, параболоид, эпюр, преподавание на младших курсах технического вуза, преподавание аналитической геометрии, преподавание инженерной графики.

Раздел: (01) отдельные вопросы сферы образования.

Основным методом аналитической геометрии служит метод координат. Основные понятия координатного метода и многие факты аналитической геометрии известны студенту первого курса из школьного курса геометрии. Изучение данного раздела геометрии в техническом вузе отличается большой строгостью и систематичностью, что предполагает тщательный отбор теоретического материала, его изложение в соответствии с основными дидактическими принципами – научности, систематичности, последовательности, доступности, наглядности; также требуется уделить особое внимание системе упражнений для развития и совершенствования умений и навыков.

«Чертеж – язык техники» – эти слова принадлежат Гаспару Монжу, основоположнику современной начертательной геометрии. Успешное освоение языка чертежа и технического рисунка является залогом формирования, развития и совершенствования пространственного воображения инженера, конструктора, дизайнера, а также базой для изучения многих дисциплин в вузе: черчения, деталей машин и механизмов, теоретической и строительной механики.

ISSN 2304-120Х

ниепт

научно-методический электронный журнал

ISSN 2Э04-120Х

ниепт

научно-методический электронный журнал

Мурашкина Т. И., Королев Е. А., Егоров А Ю. Особенности методики преподавания темы «Парабола и параболоид» в курсах математики и инженерной графики // Научно-методический электронный журнал «Концепт». -2017. – № V11. – 0,4 п. л. – URL: http://e-koncept.ru/2017/171045.htm.

Практическая деятельность будущего инженера неразрывно связана с умением представить свою идею в виде чертежа. Но чертеж – это последняя стадия конструкторской работы, а рождающаяся в сознании человека новая техническая идея требует создания математической модели, графического выражения и компьютерного представления такой идеи, то есть студенту технического университета необходимо комплексное развитие математических навыков и навыков инженерной графики. Изучение начертательной геометрии формирует и развивает геометрическое мышление, умение отображать пространственные объекты в виде рисунка, чертежа или компьютерной модели на дисплее, способствует развитию пространственного воображения, без которого невозможно никакое техническое творчество.

Для успешного усвоения указанной темы студенты должны изучить следующий теоретический материал в курсах аналитической геометрии и инженерной графики.

Парабола представляет собой геометрическое место точек плоскости, которые равноудалены от заданной точки Г и прямой б, не проходящей через Г. Это определение называется геометрическим (рис. 1).

Рис. 1

Парабола относится к линиям конических сечений, открытие которых, как полагают исследователи истории математики, принадлежит Менехму. Учение о конических сечениях развивалось Евклидом и Аполлонием Пергским, рассмотревшим в своих трудах все виды таких сечений и их свойства. Труды Аполлония примечательны тем, что представляют собой совокупность аналитической и начертательной геометрии в современном представлении.

Точка Г называется фокусом параболы, прямая б – директрисой параболы, середина О перпендикуляра, опущенного из фокуса на директрису, – вершиной параболы, расстояние р от фокуса до директрисы – параметром параболы, а расстояние р/2 -фокусным расстоянием (рис. 1). Прямую, проходящую через фокус и перпендикулярную директрисе, называют осью параболы. Отрезок ГМ, соединяющий произвольную точку М параболы с фокусом, называют фокальным радиусом точки М. Отрезок, который соединяет две точки параболы, называется хордой параболы. Отметим, что геометрическое определение выражает директориальное свойство параболы.

Существует также аналитическое определение параболы, согласно которому параболой называется линия, задаваемая уравнением вида:

y2 = 2px.

Уравнение (1) называется каноническим уравнением параболы.

ISSN 2304-120X

ниепт

научно-методический электронный журнал

Оба определения параболы, как аналитическое, так и геометрическое, равносильны. Действительно, рассмотрим следующую прямоугольную систему координат (рис. 2). Пусть вершина О параболы будет началом системы координат. Прямую, перпендикулярную директрисе, которая проходит через фокус, примем за ось абсцисс.;0) и уравнение директрисы х = -Для произвольной точки М (х, у), принадлежащей параболе, имеем: ГМ = ММь, где Мь ;у) – ортогональная проекция точки М (х, у) на директрису.

Применим формулу расстояния между точками плоскости для точек Г и М. Запишем равенство ГМ = ММь в координатной форме:

(х -1)2 + у2 = ж+|.

Возведем обе части полученного уравнения в квадрат:

(х – |)2 + у2 = х2 + р X +

Приведем подобные члены и получим каноническое уравнение параболы: у2 = 2рх (1), т. е. выбранная система координат является канонической.

При доказательстве обратного утверждения следует показать, что все точки, координаты которых удовлетворяют уравнению (1), и только они, принадлежат геометрическому месту точек, называемому параболой. Таким образом, эквивалентность аналитического и геометрического определений параболы доказана.

Рассмотрим геометрический смысл параметра р в каноническом уравнении параболы (1). Подставляя в уравнение (1) х = | , получаем: у2 = р2, т. е. у = ± р. Следовательно, параметр р – это половина длины хорды параболы, проходящей через её фокус перпендикулярно оси параболы.

Параболоидом называется тип поверхности второго порядка в трёхмерном евклидовом пространстве. Параболоид можно определить как незамкнутую нецентральную, то есть не имеющую центра симметрии, поверхность второго порядка.

ISSN 2Э04-120Х

ниепт

научно-методический электронный журнал

В декартовых координатах канонические уравнения параболоида имеют вид:

х = tx2 + иу2.

В зависимости от знаков величин £ и и, а также их равенства нулю возможны следующие типы параболоидов (табл. 1).

Таблица 1

t • u > 0 t = u t • u < 0 T = 0 или u = 0

Эллиптический параболоид Параболоид вращения Гиперболический параболоид Параболический цилиндр

Сечения параболоида вертикальными, то есть параллельными оси г, плоскостями общего положения являются параболами. Сечения горизонтальными (параллельными осям х и у) плоскостями общего положения для эллиптического параболоида представляют собой эллипсы, для гиперболического параболоида – гиперболы. Иногда сечением может оказаться прямая или пара прямых (для гиперболического параболоида или параболического цилиндра) или одна точка (для эллиптического параболоида). Рассмотрим, какие виды параболоидов существуют.

Эллиптическим параболоидом называется поверхность, определяемая в некоторой прямоугольной системе координат Oхyz каноническим уравнением:

$ + £= (2)

Гиперболическим параболоидом называется поверхность, определяемая в неко-

X2 “V2

торой прямоугольной системе координат Охуг каноническим уравнением — = 2х.

В обоих уравнениях параметры а и Ь – положительные параметры, характеризующие параболоиды, причем для эллиптического параболоида а > Ь. = 2г получим

уравнение сечения параболоида плоскостью Оуг. Данное уравнение равносильно уравнению у2 = 2цг параболы с фокальным параметром ц = Ь2. Указанные сечения называются главными параболами эллиптического параболоида.

Уравнения сечений эллиптического параболоида плоскостями, параллельными плоскости Оху, можно получить, подставляя г = Ь, где Ь – произвольная постоянная (параметр), в уравнение (2). При г = Ь получим:

4 + Й=2Л. (2′)

а2 Ь2

Возможны следующие случаи, представленные в табл. 2.

Следовательно, эллиптический параболоид можно представить как поверхность, образованную эллипсами с вершинами на главных параболах (см. рис. 3) [1-2].

Методы инженерной графики позволяют задавать поверхности черчением или рисованием, то есть графически (от греч. graphos – пишу).

Эллиптический параболоид относится к разряду так называемых нелинейчатых поверхностей (см. рис. 4). Каркас его поверхности содержит параболы и эллипсы.

ISSN 2304-120X

ниепт

научно-методический электронный журнал

Таблица 2

Знак h Л < 0 Л = 0 Л > 0

Корни (2′) X2 V2 а2 Ъ2 не имеет действительных корней х2 у2 — + 2К а2 Ъ2 имеет единственный вещественный корень х2 у2 а2 Ъ2 определяет эллипс, уравнение которого имеет вид X2 у2 — + — = 1.2К

Вид сечения Плоскость г = Л не пересекает параболоид (2) Точка О (0;0) – вершина параболоида Эллипс с центром на оси аппликат и вершинами на главных параболах

Сечения эллиптического

параболоида Параболоид вращения

Рис. 4

В инженерной графике поверхностью вращения называют поверхность, которая получается при вращении какой-либо образующей линии (прямой или кривой) вокруг неподвижной прямой. Неподвижная прямая носит название оси поверхности. В поверхности вращения, как правило, можно вписать шары с касанием по окружности. На чертеже поверхность вращения можно задать образующей и положением оси. При своем движении вокруг оси каждая точка образующей линии описывает окружность.

ISSN 2Э04-120Х

ниепт

научно-методический электронный журнал

Такие окружности называются параллелями. Плоскости, перпендикулярные к оси поверхности вращения, пересекают поверхность по параллелям.

Плоскость, проходящая через ось поверхности вращения, называется меридиа-нальной плоскостью. Как следует из названия, такая плоскость пересекает поверхность по меридиану.

На рис. 5а представлен эпюр (чертеж) параболоида вращения, а на рис. 5б – его объемно-геометрическое изображение.

Рис. 5а

Рис. 5б

В случае параболоида вращения парабола (меридиан) вращается вокруг оси i, (ilni). h{h”, h) – параллель, Meh.

В начертательной геометрии принят кинематический способ образования поверхностей. Применение данного способа подразумевает, что поверхность рассматривается как совокупность положений в пространстве движущейся линии (образующей), а закон перемещения образующей задается направляющими линиями.

Гиперболический параболоид относится к классу линейчатых поверхностей, имеющих две направляющие и плоскость параллелизма. Эти поверхности также носят название поверхностей Каталана.

Гиперболический параболоид в инженерной графике носит также название косой плоскости, а также линейчатого параболоида. Линейчатый параболоид можно получить перемещением прямолинейной образующей по двум прямолинейным направляющим, не принадлежащим одной плоскости. На рис. 6 прямые di(di”, di’) и d2(d2″, d2) являются направляющими, а прямые gi(gi”, gi*) и g2(g2n, g2′) – образующими, параллельными плоскости параллелизма ао/ (рис. 6).

Рис. 6

ISSN 2304-120X

ниепт

научно-методический электронный журнал

В аналитической геометрии доказывается, что косую плоскость, или гиперболический параболоид, можно получить в результате движения параболы ВОВ1. При этом движении ось симметрии параболы остается параллельной оси Т, вершина параболы перемещается по параболе АОА1, и плоскость параболы ВОВ1 остается параллельной плоскости ХОТ. Сечение гиперболического параболоида плоскостью, параллельной ХОУ, является гиперболой. Если такая плоскость, параллельная ХОУ, проходит через вершину О, то гиперболический параболоид пересекается по двум прямым, проходящим через точку О. Сечения гиперболического параболоида плоскостями, параллельными координатным плоскостям УОТ и ХОТ, являются параболами. Благодаря форме, гиперболический параболоид носит также название седло (рис. 7).

Рис. 7

Параболический цилиндр представлен на рис. 8. Образующая (д) и направляющая (б, парабола) парабоического цилиндра могут меняться местами друг с другом [3-9].

Рис. 8

Гиперболический параболоид и параболический цилиндр находят применение в архитектуре для создания крыш, покрытий и сводов. Так, крыша стадиона «Олимпийский» до реконструкции, а также крыша Цирка на проспекте Вернадского имеют форму гиперболического параболоида. На рис. 9 приведены проекции и аксонометрическая схема покрытия. Поверхность покрытия образована пересечением трех параболических цилиндров, имеющих общую точку О, и плоскостью, которая касается цилиндров по прямолинейным образующим, проходящим через вершины направляющих парабол. Отсеки цилиндров пересекаются по плоским кривым – параболам (рис. 9).

ниегп

issn 2304-120Х Мурашкина Т. И., Королев Е. А., Егоров А. Ю. Особенности методики преподавания темы «Парабола и параболоид» в курсах математики и инженерной графики // Научно-методический электронный журнал «Концепт». -2017. – № V11. – 0,4 п. л. – URL: http://e-koncept.ru/2017/171045.htm.

научно-методический электронный журнал

Рис. 9

Уникальные геометрические особенности параболы и параболоида обусловили их широкое применение в технике. Благодаря тому что параллельный пучок света собирается в фокусе параболы, а также если из фокуса параболы выпустить луч, то после отражения от кривой луч станет параллелен оси, параболоид вращения широко применяется в оптике. Так, форму эллиптического параболоида имеют контактные линзы. Свойства параболоида применяются и в других оптических устройствах – зеркалах, лампах, телескопах. В силу корпускулярно-волновой природы света свойства света применимы также и для электромагнитного излучения другой частоты, поэтому оптические свойства параболы были использованы в составных частях различных радиопередающих устройств, в частности узконаправленных и спутниковых антеннах, изготовляемых в основном из дюралюминия и стали (рис. 10).

Рис. 10

Из школьного курса физики известно, что тела, брошенные с поверхности земли под углом к горизонту, в поле силы тяжести (при условии, что сила вязкого трения с воздухом достаточно мала) имеют параболическую траекторию. Также такую траекторию имеют многие кометы и планеты, движущиеся в космическом пространстве вокруг массивных объектов. Упомянем также одно интересное свойство жидкостей. Например, если взять стакан с водой и начать мешать воду ложкой, то поверхность воды примет форму параболоида вращения (см. рис. 11) [10].

Изучение данного теоретического материала обязательно сопровождается решением задач. Студентам для самостоятельного решения можно рекомендовать следующие задачи.

ниепт

научно-методический электронный журнал

issn 2304-120X Мурашкина Т. И., Королев Е. А., Егоров А Ю. Особенности методики преподавания темы «Парабола и параболоид» в курсах математики и инженерной графики // Научно-методический электронный журнал «Концепт». -2017. – № V11. – 0,4 п. л. – URL: http://e-koncept.2

X2 V2 х+1

— + = z и–

5 3 2

Таким образом, объединение математических методов и методов инженерной графики при работе с учебными задачами обеспечивает глубокое понимание теоретической основы изучаемого вопроса, мотивирует студента на поиск рационального решения той или иной задачи. Межпредметные связи, устанавливаемые в процессе изучения темы «Парабола и параболоид», расширяют кругозор, способствуют формированию и развитию воображения и мышления будущего инженера.

Ссылки на источники

1. Александров А. Д., Нецветаев Н.Ю. Геометрия. – М.: Наука, 1990. – 672 с.

2. Канатников А. Н., Крищенко А. П. Аналитическая геометрия. – М.: Изд-во МГТУ им. Н. Э. Баумана, 2002. – 388 с.

3. Гервер В. А., Рывлина А. А., Тенякшев А. М. Основы инженерной графики. – М.: КноРус, 2007. -426 с.

4. Чекмарёв А. А. Инженерная графика. – М.: Юрайт, 2015. – 381 с.

5. Энциклопедия по машиностроению (XXL). – URL: http://mash-xxl.info.html.

6. Левицкий В. С. Машиностроительное черчение и автоматизация выполнения чертежей. – 9-е изд., испр. и доп. – М.: Юрайт, 2016.

7. Гильберт Д., Кон-Фоссен С. Наглядная геометрия. – М.: УРСС, 2004. – 344 с.

8. Гордон В. О., Семенцов-Огиевский М. А. Курс начертательной геометрии. – М.: Наука, 2008. – 360 с.

9. Серегин В. И., Жирных Б. Г., Шарикян Ю. Э. Начертательная геометрия. – М.: Изд-во «Москва», 2017.

10. Гельфанд И. М. и др. Функции и графики. – М.: Наука, 1968. – 96 с.

11. Сборник задач по математике для втузов / под общ. ред. А. В. Ефимова и А. С. Поспелова. – 4-е изд. – М., 2001. – 288 с.

T. Murashkina,

Candidate of Engineering Sciences, Associate Professor, Moscow State Technical University named after N. E. Bauman

[email protected]

ISSN 2Э04-120Х

ниепт

научно-методический электронный журнал

Evgeny Korolev,

Student, Moscow State Technical University named after N. E. Bauman

[email protected]

A. Egorov,

Student, Moscow State Technical University named after N. E. Bauman Sasha361 [email protected]

Features of the theme “Parabola and paraboloid” teaching methodology in the courses of mathematics and engineering graphics

Abstract. The relevance of this work relates to the special place of the lines and surfaces of the second order in the courses of analytical geometry and engineering graphics at the technical University. Parabola and corresponding to it in three-dimensional world paraboloid, play an important role in many physical processes. As a result, they have found wide application in many engineering, technical and other devices, architecture, and just in everyday life. In this article, the authors examine the mathematical properties of parabola and paraboloid and the peculiarities of their graphical representation. The content of the article will be interesting for students of engineering and mathematics, teachers of mathematics and engineering graphics, as well as for high school students preparing to enter universities to study technical or mathematical sciences, since prospects of modern school education development are associated with the growing role of its polytechnic component. Key words: parabola, paraboloid, epure, teaching junior students at technical University, analytic geometry teaching, engineering graphics teaching. References

1. Aleksandrov, A. D. & Necvetaev, N.Ju. (1990). Geometrija, Nauka, Moscow, 672 p. (in Russian).

2. Kanatnikov, A. N. & Krishhenko, A. P. (2002). Analiticheskaja geometrija, Izd-vo MGTU im. N. Je. Baumana, Moscow, 388 p. (in Russian).

3. Gerver, V. A., Ryvlina, A. A. & Tenjakshev, A. M. (2007). Osnovy inzhenernoj grafiki, KnoRus, Moscow, 426 p. (in Russian).

4. Chekmarjov, A. A. (2015). Inzhenernaja grafika, Izd-vo Jurajt, Moscow, 381 p. (in Russian).

5. Jenciklopedija po mashinostroeniju (XXLAvailable at: http://mash-xxl.info.html (in Russian).

6. Levickij, V. S. (2016). Mashinostroitel’noe cherchenie i avtomatizacija vypolnenija chertezhej. 9-e izd., ispravl. i dop., Izd-vo Jurajt, Moscow (in Russian).

7. Gil’bert, D. & Kon-Fossen, S. (2004). Nagljadnaja geometrija, URSS, Moscow, 344 p. (in Russian).

8. Gordon, V. O. & Semencov-Ogievskij, M. A. (2008). Kurs nachertatel’noj geometrii, Nauka, Moscow, 360 p. (in Russian).

9. Seregin, V. I., Zhirnyh, B. G. & Sharikjan, Ju. Je. (2017). Nachertatel’naja geometrija, Izd-vo “Moskva”, Moscow (in Russian).

10. Gel’fand, I. M. et al. (1968). Funkciiigrafiki, Nauka, Moscow, 96 p. (in Russian).

11. Efimov, A. V. & Pospelov, A. S. (eds.) (2001). Sbornik zadach po matematike dlja vtuzov, 4-e izd, Moscow, 288 p. (in Russian).

Рекомендовано к публикации:

Горевым П. М., кандидатом педагогических наук, главным редактором журнала «Концепт»

Поступила в редакцию Received 23.10.17 Получена положительная рецензия Received a positive review 10.11.17

Принята к публикации Accepted for publication 10.11.17 Опубликована Published 30.11.17

www.e-koncept.ru

977230412017311

Презентация “Парабола и я”

Просмотр содержимого документа
«Презентация “Парабола и я”»

Проект на тему: “Парабола и я”

Выполнил: Пичужкин Артём 9б

Цели проекта

Дать определение функции
Дать определение параболы
Узнать где встречаются параболы в природе
Узнать свойства параболы

Что такое функция?

Функция – это одно из основных математических и общенаучных понятий, выражающее зависимость между переменными величинами (вида y=f(x)). Что называют квадратичной функцией? Квадратичная функция — это функция вида y = ax 2 + bx + c, где a, b и с — заданные числа. При подстановке чисел вместо x получатся координаты точек(x;y), которые можно спроицировать на систему координат. Парабола с вершиной в начале координат

является графиком функции y=kx 2 .

Квадратичная функция y=x 2

Линейная функция y= ⅓ x+2

0 ( a a , а директриса — под (над) вершиной на таком же расстоянии и параллельна оси абсцисс. F- фокус “

Парабола

Пара́бола — геометрическое место точек, равноудалённых от данной прямой и данной точки.

Ось симметрии параболы, заданной квадратичной функцией, проходит через вершину параллельно оси ординат. При a 0 ( a a , а директриса — под (над) вершиной на таком же расстоянии и параллельна оси абсцисс.

F- фокус

Где встречаются параболы?

В природе

В архитектуре

Животный мир

Солнечная зажигалка

Оригинальный способ использования энергии Солнца. Солнечная зажигалка представляет собой параболическое зеркало из нержавеющей стали, почти такое же, как то, которое используется для зажигания Олимпийского огня в Афинах.

Параболическое зеркало дает возможность собрать всю энергию в одной фокусной точке и зажечь огонь. Температура в этой точке может достигать 537-ми градусов по Цельсию. Такое устройство будет незаменимо в походе и в других полевых условиях.

Легенда о том, как Архимед параболой римский флот сжёг

Согласно легенде, в 212 году до н.э., Архимед из Сиракуз сжёг флот римлян, обороняя свой город с помощью параболических зеркал. Этот день уцелевшим римлянам запомнился на всю жизнь. Почти полтысячи маленьких солнц вдруг загорелись на крепостной стене. Сначала они просто ослепляли, но через некоторое время произошло нечто фантастическое: передовые римские корабли, подошедшие к Сиракузам, один за другим вдруг начали вспыхивать, как факелы. Бегство римлян было паническим. Так для защиты своего города Архимед использовал оптическое свойство параболы

Список литературы

www.Wikipedia.ru
https://infourok.ru/nauchnoissledovatelskiy-proekt-eta-udivitelnaya-parabola-2789479.html
https ://xn--j1ahfl.xn-- p1ai/library/proekt_po_matematike_120115.html
https://xn--j1ahfl.xn-- p1ai/library/proekt_po_matematike_120115.html
Бронштейн И. Парабола
Маркушевич А. И. Замечательные кривые

Парабола Ладовского предвосхитила время – Московская перспектива

Истоки современного проекта новой Москвы прослеживаются в далеком 1930 году

Расширение территориальных границ Москвы – один из мегапроектов современной столицы, новый вектор градостроительного планирования и урбанизации территорий. Между тем, когда углубляешься в развитие современного проекта «Большая Москва», невольно возникают ассоциации с идеями, предложенными почти столетие назад. «Московская перспектива» заинтересовалась историческими параллелями.

Напомним, основной целью проекта «Большая Москва» стало стремление изменить традиционную систему Московской агломерации, упорядочить градостроительное зонирование, создав на присоединенных территориях ярко выраженную административно-правительственную специализацию.

Несмотря на амбициозный подход и новаторские решения, применяемые в ходе развития урбанистического проекта, в нем отчетливо прослеживается преемственность идеи выдающегося советского архитектора, одного из творческих лидеров рационализма Н.А. Ладовского. Именно ему принадлежит незаслуженно забытый один из ранних планов градостроительного развития Москвы, который предшествовал знаменитому Генплану реконструкции 1935 года.

Николай Александрович Ладовский считал, что в радиально-кольцевом городе кольца вынуждены разрастаться, и это неминуемо приведет к коллапсу. Он же предлагал «разомкнуть» одну из существующих окружностей и дать Москве возможность динамического развития в заданном направлении – другими словами, развивать осевое территориальное планирование.

По его мнению, Москва должна была уйти от окружностей, приняв в скором времени форму параболы, с безусловным сохранением исторического центра как ее фокуса. Осью же, согласно теории Ладовского, должна была стать Тверская улица. А со временем Москва, развиваясь в северо-западном направлении, могла бы соединиться с Ленинградом, образовав единую агломерацию с Северной столицей. Ученый акцентировал внимание на том, что центром должна выступать не точка, а именно ось – динамичная линия, вектор. Таким образом, в конце концов центр имел шансы приобрести форму веера – область, растущую вместе с городом, отвечающую запросам агломерации.

Впервые «парабола» Ладовского была опубликована в 1930 году вместе с его статьей, где архитектор давал теоретическое обоснование принципиально новой планировочной схемы развивающегося города. Согласно теории, центр развивался по оси параболы, к нему примыкали жилые районы, за которыми уже размещались промышленные территории и зеленые зоны. Новая планировочная схема объединяла в себе достоинства радиально-кольцевой и поточно-функциональной схем, согласно которой промышленные предприятия должны располагаться параллельно жилой застройке, но в то же время не имела очевидных для архитектора недостатков.

Сам Ладовский рассматривал город как взаимосвязанную урбанистическую среду, не видя в нем конгломерата площадей и широких проспектов. Это видение распространилось на все уровни его подхода к структурированию городского пространства. Впоследствии именно Ладовский стал автором концепции «гибкий город», описывающей динамичное развитие городского пространства, представляющей город как растущий урбанистический организм.

В 1929 году на заседании Объединения архитекторов-урбанистов (АРУ) Ладовский представил доклад «Москва историческая и социалистическая», где обосновал принципиально новую схему роста новой Москвы. «Понятие роста не может быть сведено к механическому увеличению территорий, ширины проездов, этажности и т.п. Рост надо понимать как органический, на разных этапах своего развития представляющий различный не только количественно, но и качественно организм. Между тем все имеющиеся до настоящего времени проекты «Большой Москвы» рассматривают вопрос исключительно с количественной стороны и потому страдают основным пороком – механичностью», – говорил Ладовский.

Архитектор использовал свою «параболу» в конкурсном проекте на реконструкцию Москвы 1932 года. Тогда проект вызвал широкий интерес, многие коллеги отмечали оригинальность мысли, предложенных идей. Однако проект Ладовского оказался невостребованным – сталинский Генеральный план реконструкции Москвы закрепил уже устоявшуюся кольцевую структуру. «Параболу» Ладовского признали нереалистичной, автора обвинили в формализме, а новые растущие районы Москвы продолжили наращивать по радиально-кольцевому принципу.

В Москве сохранился памятник незаурядной инженерной мысли советского архитектора. Николай Александрович был одним из авторов, работающим над архитектурным обликом первой линии Московского метрополитена, открытой 15 мая 1935 года. В частности, по его проекту был построен южный вестибюль станции метро «Красные Ворота» Сокольнической линии.

Уличный павильон построен в форме сложного портала, состоящего из четырех полуокружностей, сильно напоминающих чертежи его знаменитой урбанистической «параболы»: Центральная арка – это стена Московского Кремля, над ней Китайгородская, затем Бульварное кольцо, а сверху – Садовое. Официальная же версия представляет павильон как образ тоннеля метро в перспективе. По мнению современных архитекторов, облик наземного павильона станции «Красные Ворота» выглядит современно и лишен связей с исторической архитектурой, что выгодно отличает его от ряда других примеров той же Сокольнической линии.

В 1960-е годы «парабола» Ладовского проявилась в концепции греческого архитектора Константиноса Доксиадиса, который в основу своего «динаполиса» заложил планировочную схему Ладовского, сославшись на труды отечественного архитектора и опубликовав в мировой печати сообщение о «динамичных городах» Ладовского.

Очевидно, что одна из приоритетных задач урбанистов нашего времени – развить и дополнить уникальные планы людей, стоящих у истоков строительства новой Москвы, чьи идеи опередили свое время.

архитектурные светильники по проекту Гектора Эсраве

Мексиканский дизайнер Гектор Эсраве (Héctor Esrawe) разработал новую коллекцию скульптурных светильников Parábola.

Для дизайнера Эсраве это первая самостоятельно созданная коллекция света. Получившая имя Parábola, она названа в честь знаменитых параболических архитектурных конструкций испано-мексиканского архитектора Феликса Канделы. Как и у творений великого предшественника, у светильников Parábola свет работает по принципу отражения, путешествуя вдоль твёрдой поверхности и подчёркивая её собственные формы. Волны и искривления, составляющие корпус светильников, рождают уникальные светотеневые эффекты, притягивая взгляды и заставляя рассматривать светильник со всех сторон, будто это скульптура.

Сам дизайнер называет свои светильники «поэзией теней». Для него тёмные зоны и отсутствие света в этих моделях так же актуальны, как и его присутствие. «Путешествие» начинается в основании светильника, в котором закреплены медные полоски и тонкие светодиодные модули. Затем свет отражается внутри корпуса, проходя по закруглённым медным листам и создаёт приятное теплое освещение в комнате. Количество металлических полос соответствует количеству светодиодных элементов: в разных светильниках Parábola их от одного до четырёх.

Светильники Parábola безусловно очень атмосферны, но их функциональность не ограничивается только декоративными возможностями. Очень насыщенный мягкий свет задаёт тон всему интерьеру, окрашивая все объекты вокруг в себя в тёплые оттенки. Но светодиодные источники внутри достаточно мощные, чтобы подсветить и пространство вокруг.

По словам дизайнера, его новая коллекция — это «отражение света, проходящего через твердую поверхность, начало и конец, тьму и мрак вплоть до рассвета, по натяжению и изгибам, как и в параболах Феликса Канделы».

До 13 апреля светильники из коллекции Parábola можно увидеть на экспозиции новой галереи Masa в американском городе Мехико в рамках большого выставочного проекта Collective/Collectible.

Парабола в искусстве и архитектуре

Парабола – красивая и элегантная кривая. По этой причине он нравится не только математикам и физикам, но и архитекторам и инженерам. Неудивительно, что мы обнаружили, что он использовался во многих искусственных сооружениях. На этом этапе мы рассмотрим некоторые случаи появления параболы в архитектуре и дизайне.

Пара парабол, пересекающих гавань Сиднея

На изображении этого шага изображена одна из величайших икон Австралии: мост через гавань Сиднея.Построенный в 1930-х годах и охватывающий одну из величайших гаваней мира, он с видом на один из самых красивых городов мира демонстрирует две параболы в действии, но немного разных форм и размеров. мост через гавань Сиднея, загляните в интересный мир математики postPassy и мост Харбор-бридж в Сиднее. Популярный турист, который стоит посетить в Сиднее, поднимается по одной из этих параболических арок; видимо, вид весьма примечателен.

Форма подвешенного кабеля

Когда кабель подвешен между двумя точками, он принимает форму, которая очень похожа на форму параболы около вершины, называемой цепной связью.В этом случае кабель выдерживает только собственный вес. Математика цепной линии несколько более продвинута и требует понимания гиперболической функции: \ (\ normalsize cosh (x) \). Но когда подвесные тросы используются для равномерной поддержки моста, особенно тяжелого моста, как у моста Золотые Ворота в Сан-Франциско, то форма – парабола. Это еще один классический шедевр инженерной мысли. _{© «Мост Золотые Ворота» Бернарда Ганьона / Wikimedia Commons CC BY SA 3.0}

Параболические арки и купола

Арки и купола в форме парабол известны и использовались с древних времен. Они обладают особенно приятными несущими свойствами. И они по-прежнему занимают видное место в современном архитектурном дизайне. _{© «L’Oceanografic (Валенсия, Испания)» Фелипе Габальдон / Wikimedia Commons CC BY 2.0}

Поверхности, созданные из парабол

В нашем трехмерном мире поверхности часто интересуют больше, чем кривые. Математики, конечно, также интенсивно изучали поверхности второй степени, называемые квадрик : такие как сфера или эллипсоид, или гиперболоиды одного и двух листов, а также многие более сложные поверхности более высокой степени.Одна квадрика, которая является особенно тонкой, но интригующей, – это гиперболический параболоид : он приятно сочетает в себе параболы, открывающиеся в противоположных направлениях! Иногда также называется седловидной формой , по понятным причинам, это излюбленная поверхность для математически мыслящих архитекторов: _{«Седловая точка» Public Domain / Wikimedia Commons} Одним из интригующих аспектов гиперболического параболоида является то, что, хотя это полностью гладкая поверхность, это также поверхность с линейками – на самом деле это поверхность с двумя линейками, с двумя семействами линий, которые полностью лежат на ней.Вы можете сделать такую поверхность самостоятельно, если соедините соответствующие точки на двух параллельных карандашах резиновыми лентами, растяните ленты, а затем скрутите карандаши, чтобы они больше не были параллельны. Или для чего-то более постоянного, просто соедините соответствующие точки на двух фиксированных косых отрезках в пространстве с помощью нити. Поскольку гиперболическая парабола может быть построена с прямыми балками, она особенно удобна для строительства зданий. Вот железнодорожная станция Варшава-Охота. _{© «Железнодорожная станция Варшава-Охота», Панек / Wikimedia Commons CC BY SA 4.0} Другой пример – SaddleDome в Калгари, Канада. _{© «Pengrowth Saddledome», Абдаллах / Wikimedia Commons CC BY 2.0}

Вопросы для обсуждения

Знаете ли вы какие-нибудь приятные или интересные примеры парабол, используемых в архитектуре или дизайне? Мы должны задать знаменитый вопрос: являются ли арки Макдональдса параболами? Как вы думаете?

Параболическая арка – HandWiki

Параболические арки в Селлер-де-Сан-Кугат Необычное сочетание параболических и перпендикулярных готических арок в церкви Святого Марка, Бромлей, Лондон.

Параболическая арка – это арка в форме параболы.{-x}} {2}} [/ математика]. Кривые не связаны.

Линия тяги

В отличие от цепной дуги, параболическая дуга использует принцип, согласно которому при равномерном приложении веса вверху внутреннее сжатие (см. Линию тяги), возникающее в результате этого веса, будет следовать параболической кривой. Из всех типов арок параболическая арка создает наибольшую тягу в основании. Кроме того, он может охватывать самую большую площадь. Он обычно используется при проектировании мостов, где требуются длинные пролеты. ^[2] ^[3]

По сравнению с контактными дугами

Когда арка несет равномерно распределенную вертикальную нагрузку, правильной формой является парабола.Когда арка несет только собственный вес, лучшая форма – это цепная связь. ^[3]

Цепная цепь синего цвета на фоне параболы красного цвета
Парабола (красная) на фоне цепи (синяя), вид для имитации дуги.
Парабола (красная) на фоне цепной линии (синяя), вид для имитации дуги. Уменьшено.

Использует

Мемориальный кенотаф в Мемориальном парке мира в Хиросиме

Куриное яйцо можно описать как два разных параболоида, соединенных частью эллипса. .^[4] ^[5]

Соборы и церкви

Несколько примеров параболических арок:

Casa Milà ^[6] – известный пример, а
Лландаффский собор ^[7]
Церковь Святого Леонарда ^[8] ^[9]
Англиканская церковь Святого Павла ^[10]
Мемориальный кенотаф в Мемориальном парке мира в Хиросиме имеет форму параболической арки. ^[11]

Архитекторы

Параболические арки использовали архитекторы Оскар Нимейер и Антони Гауди, которые также использовали цепные арки.

Мосты и их техника

Параболические арки моста Золотые Ворота Параболическая арка моста Биксби-Крик

См. Также

Арочный мост
Катеноид
Купол
Готическая арка
Готическая архитектура
Ланцет-дуга
Ланцет окно
Математика и архитектура
Грязевые хижины мусгам
Естественная арка, в том числе цепная арка
Нубийское хранилище
ВЛ
Мост простой подвесной
Подставка стальная цепная
Ленточный мост напряженный
Подвесной мост
Фермерно-арочный мост
Убежище (архитектура)
Voussoir

Ссылки

↑ Статья из The Free Dictionary о параболической арке: Параболическая арка | Статья о параболической арке в The Free Dictionary, дата обращения: 2 марта 2017 г.
↑ Дикс, Эндрю Дж.; Хао, Хун (2004-11-15). Развитие механики конструкций и материалов . ISBN 978
↑ ^3,0 ^3,1 Проектирование предварительно напряженных бетонных мостов / Глава 17 Проектирование и строительство арок
↑ Rehkugler, G.E. (1973). «Характеризуя форму куриного яйца». Птицеводство 52 : 127–138. DOI: 10.3382 / пс. 0520127. https: // oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ps/52/1/10.3382/ps.0520127/2/poultrysci52-0127.pdf?Expires=14
295&Signature=TnS-pUPw5394lZXTqG7sWihVya-imEJYlbt5YCmO6POV8FSTakjk5MOlJd-CorsOBeJURWw1nYqD2AiZU-WmFX4TapujkJHvZ~QXKaPqsT1YloE6tcwx~ A4DNJvz0k6Vfum8wloctVh2smgvnZBFckKsZS3mLvJp6CZnY5m9VbSpC-Nj2wHoC4IIMCNIDGfuJ ~ ЗБР ~ YIpoypF6hLsUKPLTOtajnR8unfinOCIcQMEHkur4YvLJOP Ур ~ TCX ~ 2JemMj7BJIKta5dGpCyqib9ZHEwNZpgaRKE8ALj3unNQCPe4vJSYNg64digA3B-31gXJjC2qafiRhGWSWnZxwem-РЭБ __ & Key-Pair-Id = APKAIUCZBIA4LVPAVW3Q.Проверено 22 марта 2017 года.
↑ Google Книги: https://books.google.co.uk/books?id=CIAAAAAAMAAJ&pg=PA264&lpg=PA264&dq=”hen’s+egg”+”parabolic+arch”&source=bl&ots=uOzbRBeDwm&sig=ohyUSTlHqUs&sig=8gUSTlHqUsig=8gustlHqUsig=8gustlHqUsig=8gUSTl y # v = onepage & q = “куриное яйцо” “параболическая арка” & f = false, дата обращения: 22 марта 2017 г.
↑ TripAdvisor: Параболическая арка, поддерживающая крышу дома Мила – Изображение Ла Педрера, Барселона – TripAdvisor, дата обращения: 2 марта 2017 г.
↑ RIBA: Кафедральный собор Лландафф, Кардифф: неф с статуями Якоба Эпштейна, опирающийся на бетонные параболические арки | RIBA, дата обращения: 2 марта 2017 г.
↑ Интерьер церкви св. Леонарда, св… (C) Джулиан П. Гаффогг :: География Великобритании и Ирландии: Интерьер церкви Святого Леонарда, св. … (C) Джулиан П. Гаффогг :: География Великобритании и Ирландии, дата обращения: 2 марта 2017 г.
↑ Орган, Приходская церковь Святого Леонарда (C) Джулиан П. Гаффогг :: География Ирландии: пункт, дата обращения: 3 марта 2017 г.
↑ Правительство Квинсленда: Англиканская церковь Святого Павла | Окружающая среда, земля и вода | Правительство Квинсленда, дата обращения: 2 марта 2017 г.
↑ «Искусство, культура и общество Дальнего Востока».Modello Fantastico. https://higashishinbun.blogspot.com/2008/04/lultimo-sogno-di-citt-ideale-tange.html. Дата обращения 8 декабря 2016.
↑ Бисборт, Алан (10 апреля 1992 г.). «Розыгрыш мостов». The Washington Post : стр. A8 – A9.
↑ Наследие Новой Зеландии: www.heritage.org.nz/the-list/details/5180, дата обращения: 3 марта 2017 г.
↑ The New York Times: параб, дата обращения: 3 марта 2017 г.
↑ Berlin Iron Bridge Company: Berlin Iron Bridge Company, дата обращения: 4 марта 2017 г.
↑ Мост Биксби Крик на Первом шоссе из коллекции фотографий Пэта Хэтэуэя: Мост Биксби Крик на Первом шоссе из коллекции фотографий Пэта Хэтэуэя, дата обращения: 6 марта 2017 г.
↑ Стиль и народный язык: Путеводитель по архитектуре округа Лейн, штат Орегон .Western Imprints, Пресса Исторического общества Орегона. 1983. с. 151. ISBN 978-0-87595-085-3.
↑ Alamy: para, дата обращения: 4 марта 2017 г.
↑ Парабола моста Золотые Ворота, Сильвия Стагно на Прези: Парабола моста Золотые Ворота, Сильвия Стагно на Прези, дата обращения: 4 марта 2017 г.
↑ Mathematics Stack Exchange: berli, дата обращения: 4 марта 2017 г.
↑ «Проект моста через арку Хьюм». Arup. Архивировано 23 марта 2006 года. Https: //web.archive.org / web / 20060323201013 / http: //www.arup.com/europe/project.cfm? pageid = 190. Проверено 3 марта 2017 года.
↑ Красноярский мост: параб, дата обращения: 4 марта 2017 г.
↑ Фотографии Джин МакКоночи на pbase.com: пункт, дата обращения: 3 марта 2017 г.
↑ Arch Bridges на Waymarking.com: Memorial Bridge – Springfield / West Springfield, MA – Arch Bridges на Waymarking.com, дата обращения: 4 марта 2017 г.
↑ Смит 2001, стр. 38
↑ Химено и Гутьеррес. стр.122
↑ Параболы в подвесных мостах! О боже !: parab, дата обращения: 4 марта 2017 г.
↑ Почему кабели, соединяющие башни в подвесном мосту, имеют форму параболы? Это лучше со структурной точки зрения или чисто эстетически? : askscience: Почему кабели, соединяющие опоры в подвесном мосту, имеют форму параболы? Это лучше со структурной точки зрения или чисто эстетически? : askscience, дата обращения: 4 марта 2017 г.
↑ «Тайн-Бридж».24 сентября 2014 г. https://www.bbc.co.uk/insideout/northeast/series3/tyne_bridge_northeasthistory.shtml. Проверено 3 марта 2017 года.
↑ Мост у водопада Виктория: К водопаду Виктория – Мост у водопада Виктория, дата обращения: 2 марта 2017 г.
↑ Livingstone News: в центре, дата обращения: 2 марта 2017 г.
↑ Best Bridge Africa Мост к водопаду Виктория: Лучший мост в Африке Мост к водопаду Виктория, дата обращения: 2 марта 2017 г.

Внешние ссылки

Библиография

(PDF) Парабола параболической арки

“… строительных структурных организмов, сформированных законами статики, которые, благодаря этому, обретают

красноречие и формальную выразительность, что позволяет нам вернуться к архитектурной истине [8] .

Нерви признает, что это не относится к более простым структурам, где архитектор может выбрать

любую строительную систему, но его видение – одно из «ясной и честной конструктивной искренности», где

поэзия рождается из послушания «величественная вечность» «таинственных законов природы». Этот мистицизм

, граничащий с религией, является ответом Нерви на страх перед архитектурой, в которой преобладает холодный разум, и имеет сходство с взглядом Гауди на структуры как на отражение божественный разум.Реализация этих принципов

может быть найдена во многих сводчатых помещениях, спроектированных Нерви за

тридцать лет. Ангары в Орбетелло и Орвието, Италия, были построены с системой легких нервюр

, опирающихся на параболические арки, укрепленные на земле. Бетонные ребра (образующие диагриду, которую Нерви назвал

«геодезической») выглядят как готические арки при пересечении по углам (рис. 6 и 7).

Рис. 6: Ангар в Орвието, Италия, 1935-1936 гг.Пьер Луиджи Нерви

Рис. 7: Ангар в Орбетелло, Италия (цифровая модель), 1939-41 гг. Pier Luigi Nervi

Все своды Nervi используют параболические арки в качестве основной системы с упором на систему опор

, например, в зале C Туринской выставки. В итоге Нерви собрал усовершенствованный репертуар из

эффективных конструктивных решений, разработанных путем экспериментов и расчетов, которые он

адаптировал к различным функциональным программам.В этом Нерви ближе, чем он мог подумать, к раннему готическому способу строительства

, принимая знакомые типологии и бросая вызов ограничению пролета

, непрерывно совершенствуя технологии строительства.

3. Испанская траектория современной готики

Использование параболы в качестве ссылки на готическую архитектуру связывает Гауди, Феликса Кандела и

Сантьяго Калатрава, все они родились и обучались в Испании. Влияние Гауди, Канделы, а также Нерви

на Калатраву было признано в течение некоторого времени несколькими историками и критиками [9].С технологической точки зрения

, Феликс Кандела также находился под влиянием Эдуардо Торроха, испанского инженера

, который был одним из первых, вместе с Робертом Майяртом, который экспериментировал с тонкими бетонными оболочками в

1930-х годов [10]. Распространение параболических оболочек в архитектуре в основном связано с Феликсом Канделой, который

переехал из Испании в Мексику в 1940-х годах. Кандела привлек внимание своим дизайном оболочек с двойной кривизной

, точнее гиперболических параболоидов, которые он применил к множеству зданий.

Церковь Медалла Милагроса в Канделе, построенная

между 1953 и 1955 годами в Наварте, Мехико (рис.

8), сравнивают с работой Антона Гауди, который

использовал гиперболические параболоиды в капелле Гуэля. а в

– Саграда Фамилия. Идея этой церкви пришла к

Канделе из французского инженерного текста, где он увидел структуру

, образованную четырьмя параболоидами

“, образующими четыре грани, очень заостренные, и это дало мне представление

о том, что с параболоидами я мог бы

сделать эти формы восходящей тенденции

, что действительно готическое, и это то, что считается

западной религиозной архитектурой [11].”

Отголоски этих идей сегодня можно найти в Сантьяго.

Рис. 8: Церковь Медалла Милагроса, Наварте,

Мехико, 1953-1955 гг. Феликс Кандела

Почему параболы используются в архитектуре

Математические кривые, такие как парабола, не были изобретены. Скорее, они были обнаружены, проанализированы и использованы. Парабола имеет множество математических описаний, имеет долгую и интересную историю в математике и физике и сегодня используется во многих практических приложениях.

Парабола – это непрерывная кривая, которая выглядит как открытая чаша, стороны которой бесконечно поднимаются вверх. Одно из математических определений параболы – это набор точек, которые находятся на одинаковом расстоянии от фиксированной точки, называемой фокусом, и линии, называемой направляющей. Другое определение состоит в том, что парабола – это определенное коническое сечение.

Это означает, что вы увидите кривую, если рассечете конус. Если вы разрежете параллельно одной стороне конуса, вы увидите параболу. Более общее уравнение существует и для других ситуаций.Греческий математик Менахм в середине четвертого века до нашей эры также приписывают использование парабол для решения проблемы нахождения геометрического построения кубического корня из двух.

Менахм не смог решить эту проблему с помощью конструкции, но он показал, что вы можете найти решение, пересекая две параболические кривые. Греческий математик Аполлоний Пергский с третьего по второй век до нашей эры. Однако математическая природа общей траектории движения снаряда не была известна.С появлением пушек это стало важной темой. Признавая, что горизонтальное движение и вертикальное движение независимы, Галилей показал, что снаряды движутся по параболическому пути.

Параболический отражатель может фокусировать или концентрировать энергию, идущую прямо на него. Спутниковое телевидение, радары, вышки сотовой связи и звукосниматели – все используют фокусирующие свойства параболических отражателей. Огромные радиотелескопы концентрируют слабые сигналы из космоса для создания изображений далеких объектов, и сегодня используется множество огромных радиотелескопов.Светоотражающие телескопы также работают по этому принципу: каждый раз, когда поверхности комнаты фокусируют отраженный от них звук, они создают пятна высокой интенсивности и другие точки низкой интенсивности.

Обычно это нежелательно в зале, так как требуется однородный, равномерно распределенный звук для всех слушателей. Следует избегать даже больших плоских отражающих поверхностей из-за сильного отражения, которое будет производиться.

Параллельные плоские стены могут создавать картину отражений, известную как «флаттер-эхо», когда звуковые волны перемещаются вперед и назад между поверхностями.Такое флаттер-эхо часто встречается в гимназиях средней школы, где есть параллельные боковые стены, а также светоотражающие пол и потолок. Равномерная дисперсия настолько важна для хорошей акустики, что иногда желательно использовать антифокусные поверхности в зоне создания музыки.

В более старой архитектуре часто использовались колонны, декоративная скульптура, изделия из дерева и другие рассеивающие поверхности. В современной архитектуре с ее плоскими просторами необходимо предусмотреть некоторые антифокусные свойства.Эллипс имеет две точки фокусировки. Звук, проецируемый в любом направлении из одной точки фокусировки, переместится в другую. Звук из любой точки будет иметь тенденцию быть сосредоточенным в какой-то точке, поэтому в большинстве акустических целей следует избегать использования эллипсов. Затем, совершенно случайно, кто-то обнаружил, что за высоким алтарем в ногах вдали отчетливо слышен ропот исповеди.

Конфигурация стен за алтарем фокусировала звуковые волны из точки на другом конце собора, хотя люди между ними ничего не слышали.Это полезно для проецирования звука. Две параболы, показанные ниже, могут с большой эффективностью направлять звук от точки фокусировки одной к точке фокусировки другого.

Микрофонный элемент можно поместить в точку фокусировки параболы, а затем направить на удаленный источник звука – параболические микрофоны могут улавливать выбранные звуки на удивительных расстояниях. Популярная практика в здании Капитолия в Вашингтоне, округ Колумбия. Обычный разговор может быть, если говорящий и слушающий находятся близко к стене купола.Многие здания с куполообразными ротондами демонстрируют это управляемое явление отражения. Места, где ощущается эффект ротонды, иногда называют «шепчущими галереями».

Купол собора Святого Павла в Лондоне – известный пример. Нефокусирующие поверхности Каждый раз, когда поверхности комнаты фокусируют отраженный от них звук, они создают пятна с высокой интенсивностью и другие точки с низкой интенсивностью. Index Auditorium акустика. Сфокусированные отражения. Щелкните любую геометрическую фигуру для получения дополнительных сведений.Влияние отражений на акустику. Эллиптический корпус Эллипс имеет две точки фокусировки.

Параболические поверхности. Все лучи от фокуса параболы до ее поверхности будут направлены наружу как параллельные лучи. Эффект ротонды Популярная практика в U. Антифокусирующие поверхности Поскольку в зале очень желательно даже рассеивание звука, может потребоваться принять меры для преодоления любых поверхностей фокусировки.

Если архитектор решит, что по какой-то причине желательна некоторая криволинейная поверхность, то нежелательный эффект фокусировки можно частично преодолеть, закрыв криволинейную поверхность антифокусирующими поверхностями.Парабола – это вытянутая U-образная геометрическая форма. Это можно сделать, разрезав конус. Параболы можно увидеть в природе или в искусственных предметах. Эта геометрическая форма широко распространена и даже помогает фокусировать свет и радиоволны, от дорожек, где забрасываются бейсбольные мячи, до спутниковых антенн и фонтанов.

Параболы можно увидеть повсюду, как в природе, так и в искусственных предметах. Рассмотрим фонтан. Вода, взметнувшаяся фонтаном в воздух, падает по параболической траектории. Подброшенный в воздух мяч также следует параболической траектории.Галилей продемонстрировал это. Даже архитектурные и инженерные проекты раскрывают использование парабол. Параболические формы можно увидеть в Параболе, построенном в Лондоне строении, которое может похвастаться медной крышей с параболическими и гиперболическими линиями.

Параболы также обычно используются, когда необходимо сфокусировать свет. На протяжении веков маяки претерпевали множество изменений и улучшений в свете, который они могли излучать. Плоские поверхности слишком сильно рассеивали свет, чтобы быть полезными для моряков.

Сферические отражатели увеличивали яркость, но не могли дать мощный луч.Но использование отражателя в форме параболы помогло сфокусировать свет в луч, который можно было увидеть на большом расстоянии. Первые известные параболические отражатели для маяков легли в основу маяка в Швеции. Со временем будут реализованы многие различные версии параболических отражателей с целью уменьшения потерь света и улучшения поверхности параболы.

В конце концов, стеклянные параболические отражатели стали предпочтительнее, и когда появилось электрическое освещение, комбинация оказалась эффективным способом обеспечения маячного луча.То же самое и с фарами. Стеклянные автомобильные фары с герметичным светом от s до s использовали параболические отражатели и стеклянные линзы для концентрации лучей света от ламп, улучшая видимость при вождении.

Позже более эффективные пластиковые фары могли иметь такую форму, что линзы не требовались. Эти пластиковые отражатели сегодня широко используются в фарах. Использование параболических отражателей для концентрации света теперь помогает солнечной энергетике. Конструкция парабол описывается уравнениями X и Y.

Параболы используются, потому что у них есть кривые, которые легко построить математически. Параболы в архитектуре – это учебный материал, который следует усвоить многим архитекторам.

Многие великие достопримечательности используют это здание, чтобы придать ему великолепный вид и создать ощущение антиквариата. Параболы использовались в эпоху барокко и ренессанса. Он использовался много лет назад, чтобы здание выглядело элегантно с кривыми параболами. Это было просто потому, что архитекторы тоже занимаются математикой, чтобы здание с параболой выглядело симметрично и круто.

Параболы используются в архитектуре для придания формы зданию, например, воротам или крыше. Крыша некоторых замечательных достопримечательностей обычно имеет форму парабол, потому что она выглядит менее резкой, чем придает крыше гладкости.

Это поможет вам узнать о параболах в архитектуре, чтобы вы могли знать, в чем именно заключается их функция. Эта тема поста: Архитектура. Makeover Drop Leaf кухонный стол. Кровать-чердак Hip Ideas с горкой. Значение белого кухонного стола.

Изготовление архитектурных моделей. На этом сайте используются файлы cookie. Нет проблем Подробнее. Парабола – красивая и элегантная кривая. По этой причине он нравится не только математикам и физикам, но и архитекторам и инженерам. Неудивительно, что мы обнаружили, что он использовался во многих искусственных сооружениях. Подробное обсуждение математики моста через гавань Сиднея можно найти в интересном посте. Популярное туристическое занятие в Сиднее – подъем по одной из этих параболических арок; видимо, вид весьма примечателен.

Математика цепной связи несколько более продвинута и требует понимания гиперболической функции :. Но когда подвесные тросы используются для равномерной поддержки моста, особенно тяжелого, как мост Золотые Ворота в Сан-Франциско, тогда форма представляет собой параболу.

Еще один классический шедевр инженерной мысли. Арки и купола в форме парабол были известны и использовались с древних времен. Они обладают особенно приятными несущими свойствами.

И они по-прежнему занимают видное место в современном архитектурном дизайне. В нашем трехмерном мире поверхности часто интересуют больше, чем кривые. Математики, конечно, также интенсивно изучали поверхности второй степени, называемые квадриками: такие как сфера, или эллипсоид, или гиперболоиды одного и двух листов, а также многие более сложные поверхности более высокой степени.

Одна квадрика, которая является особенно тонкой, но интригующей, – это гиперболический параболоид: он приятно сочетает в себе параболы, открывающиеся в противоположных направлениях! Иногда по понятным причинам также называют седловидной формой, это излюбленная поверхность для математически мыслящих архитекторов:

Один из интригующих аспектов гиперболического параболоида состоит в том, что, хотя это полностью гладкая поверхность, это также линейчатая поверхность – на самом деле это поверхность с двумя линейками, на которой полностью лежат два семейства линий.Вы можете сделать такую поверхность самостоятельно, если соедините соответствующие точки на двух параллельных карандашах резиновыми лентами, растяните ленты, а затем скрутите карандаши, чтобы они больше не были параллельны.

Или для чего-то более постоянного, просто соедините соответствующие точки на двух фиксированных наклонных отрезках в пространстве с помощью резьбы. Поскольку гиперболическая парабола может быть построена с прямыми балками, она особенно подходит для строительства зданий. Знаете ли вы какие-нибудь приятные или интересные примеры парабол, используемых в архитектуре или дизайне? Арка может быть синонимом свода, но свод можно выделить как непрерывную арку, образующую крышу.

Арки появились еще во 2-м тысячелетии до нашей эры в месопотамской кирпичной архитектуре, и их систематическое использование началось с древних римлян, которые первыми применили эту технику к широкому кругу структур. Арки также могут быть сконфигурированы для создания сводов и аркад.

Параболы в искусстве и архитектуре

Древнеримские строители в значительной степени полагались на закругленную арку для перекрытия больших открытых пространств. Несколько закругленных арок, расположенных в ряд, встык, образуют аркаду, такую как римский акведук.

Пример полукруглой арки с использованием известняковых блоков у Великой китайской стены. Римский акведук недалеко от Нима, Франция. Пример аркады, использующей круговую арку. Преимущество использования заостренной арки, а не круглой, состоит в том, что действие дуги в заостренной арке создает меньшую тягу к основанию. Это нововведение позволило создать более высокие и более близко расположенные проемы, типичные для готической архитектуры.

Собор Св. Михаила и Св. Внутренний сводчатый потолок Нотр-Дам де Пари, демонстрирующий ребра на пересечении нескольких арок.

Примеры параболы из реальной жизни

Из всех типов арок параболическая арка создает наибольшую тягу в основании, но может охватывать самые большие площади. Он обычно используется при проектировании мостов, где требуются длинные пролеты.

Форма кривой, прорисовываемой свободным отрезком цепи или веревки, контактная сеть – структурно идеальная форма для отдельно стоящей дуги постоянной толщины. Сегментарная дуга или меньше полукруга. Истинные арки, в отличие от арок-выступов, были известны ряду цивилизаций на Древнем Ближнем Востоке и в Леванте, но их использование было нечастым и в основном ограничивалось подземными сооружениями, такими как водостоки, где проблема бокового удара значительно уменьшилась.

Редкое исключение – арочные городские ворота бронзового века в современном Израиле Ашкелон, датируемые ок. Ранний образец арки вуссуар появляется в пешеходном мосту на греческом Родосе. Арки Corbel были найдены в других частях древней Азии, Африки, Европы и Америки. Робот Ина обнаружил длинный коридор с арочной крышей под пирамидой Кецалькоатля в древнем городе Теотиуакан к северу от Мехико, датируемый примерно нашей эрой.

Древние греки представили арку на итальянском языке, которую сегодня можно увидеть на юге полуострова и на Сицилии.Древние римляне узнали арку от этрусков, усовершенствовали ее и были первыми строителями, которые полностью раскрыли ее потенциал для строительства наземных построек: Римляне были первыми строителями в Европе, возможно, первыми в мире, которые полностью оценили преимущества арки, свода и купола. По всей Римской империи их инженеры возводили арочные конструкции, такие как мосты, акведуки и ворота.

Ввели триумфальную арку как военный памятник. Своды начали использоваться для кровли больших внутренних пространств, таких как залы и храмы, функция, которую также выполняли купольные сооружения с 1 века до нашей эры.

Они также обычно использовались при строительстве домов, как в Остии Антика, см. Рисунок. Первый образец ранней готической арки в Европе установлен на Сицилии в греческих укреплениях Гелы. За полукруглой аркой в Европе следовала остроконечная готическая арка или огив, центральная линия которой более точно соответствовала силам сжатия и поэтому была сильнее.

Полукруглая арка может быть сплющена в эллиптическую арку, как на мосту Санта-Тринита. Как параболическая, так и цепная арки теперь известны как теоретически самые прочные формы.Контактная и параболическая арки переносят всю горизонтальную тягу на фундамент и поэтому не нуждаются в дополнительных элементах. Первые образцы остроконечной арки в европейской архитектуре находятся на Сицилии и относятся к арабо-нормандскому периоду.

Подковообразная арка основана на полукруглой арке, но ее нижние концы продолжаются дальше по окружности, пока они не начнут сходиться. Параболы представляют собой набор точек в одной плоскости, которые образуют U-образную кривую, но применение этой кривой не ограничивается миром математики.

Его также можно увидеть в предметах и вещах вокруг нас в повседневной жизни. ScienceStruck перечисляет некоторые примеры из реальной жизни и их важность, которые помогут вам лучше понять эту кривую.

* Параболы в архитектуре *?

Путь объекта, брошенного или подброшенного в воздух, образует параболу. Первым это доказал Галилей. В начале 17 века он экспериментировал с шариками, катящимися по наклонным плоскостям. Парабола – это двумерная фигура в форме буквы U.Эту кривую можно описать как геометрическое место точек, где каждая точка кривой находится на одинаковом расстоянии от фокуса и направляющей.

Мы не можем назвать любую U-образную кривую параболой; Важно, чтобы каждая точка на этой кривой была равноудалена от фокуса и направляющей. Вот рисунок, который поможет вам лучше понять концепцию параболы. Параболы тоже имеют разные особенности. Если материал, отражающий свет, имеет форму параболы, световые лучи, параллельные его оси симметрии, будут отражаться в его фокус, независимо от того, где происходит отражение.И наоборот, если свет исходит из фокуса, он будет отражаться в виде параллельного луча, параллельного оси симметрии.

Эти принципы работают для света, звука и других форм. Это свойство очень полезно во всех примерах, встречающихся в реальном мире. Спутниковая тарелка – прекрасный пример отражающих свойств парабол, упомянутых ранее.

Полученные сигналы направляются непосредственно в фокус, которые затем правильно отражаются на приемник, сигналы отправляются параллельно оси.Эти сигналы затем интерпретируются и передаются как каналы на нашем телевизоре. Тот же принцип применим и к радиочастотам. Параболические зеркала заднего вида и обогреватели также работают по тому же принципу.

Это тот же принцип, что и в фонаре. Внутренняя поверхность гладкая и сделана из стекла, что делает его мощным отражателем. Используемый здесь принцип заключается в том, что источник света находится в фокусе, и световые лучи будут отражаться параллельно оси. По этой причине можно увидеть толстый сфокусированный луч света, излучаемый фарами.

Существуют специальные линзы с призмами для отклонения прямых лучей. Если рассматривать подвесные мосты, форма тросов, на которых они подвешены, напоминает параболическую кривую. Существует достаточная путаница в отношении того, подвешены ли кабели по параболе или по цепной линии. Исследования показывают, что форма ближе к параболе.

Сложная геометрия исламского дизайна – Эрик Броуг

Тросы были бы гиперболическими, но при равномерной нагрузке на горизонтальный настил они деформируются как парабола.Возьмем, к примеру, любой объект, подброшенный в воздух. Он поднимается в воздух до наивысшей достижимой высоты или точки, а затем снова опускается на землю. Если нужно проследить путь объекта, полученная кривая будет параболой. Точка, в которой вы отпускаете мяч, и высота образуют линию оси Y на графике.

Середина этой прямой делится пополам перпендикуляром от вершины параболы.

примеров параболы из реальной жизни | Наука

Обновлено 6 ноября 2020 г.

Дж.2

TL; DR (слишком долго; не читал)

Параболы можно увидеть в природе или в искусственных предметах. Эта геометрическая форма широко распространена и даже помогает фокусировать свет и радиоволны, от дорожек, где забрасываются бейсбольные мячи, до спутниковых антенн и фонтанов.

Повседневные параболы

Параболы можно увидеть повсюду, как в природе, так и в искусственных предметах. Рассмотрим фонтан. Вода, взметнувшаяся фонтаном в воздух, падает по параболической траектории.Подброшенный в воздух мяч также следует параболической траектории. Галилей продемонстрировал это. Кроме того, любой, кто катается на американских горках, знаком с подъемом и падением, создаваемым параболами трассы.

Параболы в архитектуре и проектировании

Даже архитектурные и инженерные проекты раскрывают использование парабол. Параболические формы можно увидеть в лондонском здании Parabola, построенном в 1962 году, которое может похвастаться медной крышей с параболическими и гиперболическими линиями.Знаменитый мост Золотые Ворота в Сан-Франциско, Калифорния, имеет параболы на каждой стороне боковых пролетов или башен.

Использование параболических отражателей для фокусировки света

Параболы также обычно используются, когда свет необходимо сфокусировать. На протяжении веков маяки претерпевали множество изменений и улучшений в свете, который они могли излучать. Плоские поверхности слишком сильно рассеивали свет, чтобы быть полезными для моряков. Сферические отражатели увеличивали яркость, но не могли дать мощный луч.Но использование отражателя в форме параболы помогло сфокусировать свет в луч, который можно было увидеть на большом расстоянии. Первые известные параболические отражатели для маяков легли в основу маяка в Швеции в 1738 году. Со временем будет реализовано множество различных версий параболических отражателей с целью уменьшения потерь света и улучшения поверхности параболы. В конце концов, стеклянные параболические отражатели стали предпочтительнее, и когда появилось электрическое освещение, комбинация оказалась эффективным способом обеспечения маячного луча.

То же самое и с фарами. Стеклянные автомобильные фары с герметичным светом в 1940–1980-х годах использовали параболические отражатели и стеклянные линзы для концентрации лучей света от ламп, что улучшало видимость при вождении. Позже более эффективные пластиковые фары могли иметь такую форму, что линзы не требовались. Эти пластиковые отражатели сегодня широко используются в фарах.

Использование параболических отражателей для концентрации света теперь помогает солнечной энергетике. Плоские фотоэлектрические системы поглощают солнечный свет и свободные электроны, но не концентрируют его.Однако изогнутое фотоэлектрическое зеркало может гораздо более эффективно концентрировать солнечную энергию. Огромные изогнутые зеркала составляют огромную солнечную установку с параболическим желобом в Хила-Бенд, Солана. Солнечный свет фокусируется параболическим зеркалом таким образом, что он выделяет очень сильное тепло. Это нагревает трубки синтетического масла у желоба каждого зеркала, которое затем может либо генерировать пар для энергии, либо храниться в массивных резервуарах с расплавленной солью для хранения энергии на будущее. Параболическая форма этих зеркал позволяет накапливать и производить больше энергии, что делает процесс более эффективным.

Параболы в космическом полете

Мерцающая растянутая дуга запуска ракеты – это, пожалуй, самый яркий пример параболы. Когда запускается ракета или другой баллистический объект, он следует по параболическому пути или траектории. Эта параболическая траектория использовалась в космических полетах на протяжении десятилетий. Фактически, самолеты могут создавать среду с нулевой и высокой гравитацией, летая по параболам. Специальные самолеты летают под крутым углом, создавая ощущение более высокой гравитации, а затем падают в так называемое свободное падение, создавая ощущение невесомости.Такие испытания прошел летчик-испытатель Чак Йегер. Это обеспечило огромные исследования как для пилотов-людей, так и для их терпимости к космическим полетам и полетам с разной силой тяжести, к выполнению экспериментов, требующих низкой гравитации или невесомости. Такие параболические полеты экономят деньги, поскольку им не нужно проводить каждый эксперимент в самом космосе.

Другое применение парабол

Рассмотрим спутниковую антенну. Эти структуры имеют параболическую форму, что позволяет отражать и фокусировать радиоволны.

Электроны могут искривляться точно так же, как свет. Было обнаружено, что пучки электронов могут проходить через голографическую пленку и параболически изгибаться вокруг барьеров. Это лучи Эйри, они не блекнут и не дифрагируют. Эти лучи могут оказаться полезными при визуализации.

Параболы можно увидеть повсюду, от космических полетов и автомобильных фар до мостов и парков развлечений. Парабола имеет не только элегантную геометрическую форму, но и ее функциональные возможности во многом помогают человечеству.

Знаменитые параболические арки и архитекторы – Параболические арки

Триумфальная арка, Париж, Франция – Один из самых известных памятников Парижа. Он стоит на западной оконечности Елисейских полей и чтит тех, кто сражался и погиб за Францию во французских революционных и наполеоновских войнах, с именами всех французских побед и генералов, начертанными на его внутренней и внешней поверхности. Он был построен в 1806-1836 годах и имеет высоту 50 метров (164 фута).Памятник спроектировал Жан Шалгрин.

Триумфальная арка, Париж, Франция Жан Шалгрин

The Gateway Arch, Сент-Луис, США – 630-футовый (190 м) памятник в Сент-Луисе, штат Миссури . Облицованный нержавеющей сталью и построенный в форме арки, это самый высокий рукотворный памятник в Соединенных Штатах и самая высокая арка в мире. Чтобы подняться на вершину арки, на каждой опоре арки есть трамвай.Каждый трамвай представляет собой цепочку из восьми яйцевидных отсеков, в каждом из которых может разместиться пять пассажиров. Поездка на вершину занимает четыре минуты. Арка ворот была спроектирована финско-американским архитектором Ээро Саариненом в 1947 году; Строительство началось 12 февраля 1963 года и было завершено 28 октября 1965 года за 13 миллионов долларов (что эквивалентно 180 миллионам долларов в 2013 году). Памятник открылся для посещения 10 июня 1967 года.

Арка Ворот «на самом деле является памятником 20-го века и вершины американского могущества», – говорит историк Трейси Кэмпбелл. Ээро Сааринен, финн-американец

Арка Руа Аугуста, Лиссабон, Португалия – Это историческое здание и достопримечательность в Лиссабоне было построено в ознаменование реконструкции города после землетрясения 1755 года. Строительство монумента длилось много лет – с 1755 по 1873 год. Аллегорическая группа наверху, выполненная французским скульптором Селестеном Анатолем Кальмелсом , олицетворяет Славу, вознаграждающую доблести и гения.

Rua Augusta Arch, Лиссабон, Португалия

Арка Пятидесятилетия, Брюссель, Бельгия – Арка была запланирована для всемирной выставки 1880 года в ознаменование 50-летия Бельгии как независимой страны.Однако строительство не было завершено в срок. На это ушло еще много лет, но строительство было окончательно завершено в 1905 году, как раз к 75-летию независимости Бельгии. Первоначальные павильоны выставки 1880 года, спроектированные Гедеоном Бордио, были в значительной степени заменены триумфальной аркадой, спроектированной Шарлем Жиро в 1904 году, и большими залами с обеих сторон.

Arch of Cinquantenaire, Брюссель, Бельгия

Триумфальная арка, Барселона, Испания – Триумфальная арка в столице Каталонии была построена в качестве главных ворот на Всемирную ярмарку Барселоны 1888 года.Он был построен архитектором Хосепом Виласека-и-Казановасом как главные ворота на Всемирную ярмарку Барселоны 1888 года.

Arc de Triomf, Барселона, Испания Josep Vilaseca i Casanovas

Военное время внесло серьезные изменения в технологию деревянного строительства в Австралии, особенно в дни после нападения Японии на Перл-Харбор.
В 1942 году стране угрожало вторжение. Использование древесины в гражданских целях строго контролировалось, а строительство жилых домов без согласия правительства было запрещено.Большое количество войск союзников и их массы должны были быть размещены и защищены.
Откройте для себя целый ряд стройных, прочных и изящных деревянных конструкций, ранее не известных в Австралии. Возможно, наиболее интересными были деревянные конструкции с параболическими арками, которые назывались «иглу» – в их первоначальной форме использовались, чтобы скрыть ударные самолеты, но затем эволюционировали для «размещения» всевозможного военного оборудования.
Иглу были спроектированы французским инженером Эмилем Бризе (1900-1983). После службы в Первой мировой войне он обучался в Анжере, где в 1921 году получил диплом инженера. С 1923 года он работал у первопроходца, инженера-бетонщика Юджина Фрейзеннета, возводя мост Плугастель и авиационные ангары в Виллакубле. В 1926 году Бризе получил должность в Сингапуре во французской колониальной фирме, для которой он проектировал и строил здания и мосты. С 1929 года он практиковал в частном порядке, специализируясь на бетоне и консультируя Департамент общественных работ.

Источник: http: // www.timberdesignmag.com/projects/parabolic-arches/

Нравится:

Нравится Загрузка …

Parabola Architecture выигрывает премию AIA Leading Edge Award в области архитектуры

UVA School of Architecture с гордостью сообщает, что Parabola Architecture , соучредителем которого является выпускник Кевин Берк , AIA (MArch ’87), с Кэрри Майнберг Берк, AIA, недавно был удостоен награды AIA California Leading Edge Award в области архитектуры в знак признания « Excellence in Design and Sustainability » за свой проект, Google в 1212 Bordeaux.

Созданный в прямом ответе на контекст своего сайта, 1212 Bordeaux является воплощением дизайнерской поговорки Parabola о том, что «силы развивают форму». Здание ориентировано на участке по отношению к солнцу и ветру. Внутренний двор с садом спроектирован так, чтобы приглашать солнце и блокировать дискомфорт, дующий с преобладающего бриза с залива Сан-Франциско.

Благодаря сохранению зрелой оливковой рощи на западной окраине участка и посадке местных видов, 1212 восстанавливает глубокую связь с природой.

Проект получил высокую оценку за интеграцию принципов биофильного дизайна. Приверженность Google соединению людей с природой, сформулированная в их Руководстве по биофильному дизайну, послужила основой для подхода к дизайну:

«Цель Google – создать яркое и здоровое общество, которое обогащает все живое. Мы рассматриваем людей как неотъемлемую часть природы, и наши проекты должны отражать эту точку зрения. Создавая прочные связи человека с природой в наших пространствах и сообществах, мы можем создавать впечатления, которые положительно влияют на наш разум, тело и поведение.Этот опыт должен оживить среду Google, укрепить эмоциональную связь с местами и побудить бережно относиться к нашей искусственной и природной среде “.

Выпускник Кевин Берк – признанный лидер в области комплексного проектирования. Его отмеченные наградами проекты достигли высочайшего уровня экологичности, создавая при этом вдохновляющие места для общения, взаимодействия и благополучия.

Парабола в архитектуре – математика, презентации

Параболы в арочных мостах | Обучонок

Подробнее о работе:

Оглавление

Введение

Парабола

Парабола в колокольчике

Из истории мостостроения в России с XII по XIX века

Виды мостов

Арочные мосты

Казанский мост

Арка-галерея над Зимней канавкой

Мост в Юсуповском саду

Синий мост

Троицкий мост

Заключение

Список используемых источников

Приложение 1. Казанский мост

Приложение 2. Арка-галерея над Зимней канавкой

Приложение 3. Мост в Юсуповском саду

Приложение 4. Синий мост

Приложение 5. Троицкий мост

Гиперболы, параболы, миллиметровка и… матрешки

Презентация “Парабола и я”

Парабола Ладовского предвосхитила время – Московская перспектива

архитектурные светильники по проекту Гектора Эсраве

Парабола в искусстве и архитектуре

Пара парабол, пересекающих гавань Сиднея

Форма подвешенного кабеля

Параболические арки и купола

Поверхности, созданные из парабол

Вопросы для обсуждения

Параболическая арка – HandWiki

Линия тяги

По сравнению с контактными дугами

Использует

Соборы и церкви

Архитекторы

Мосты и их техника

См. Также

Ссылки

Внешние ссылки

Библиография

(PDF) Парабола параболической арки

Почему параболы используются в архитектуре

Параболы в искусстве и архитектуре

Примеры параболы из реальной жизни

* Параболы в архитектуре *?

примеров параболы из реальной жизни | Наука

TL; DR (слишком долго; не читал)

Повседневные параболы

Параболы в архитектуре и проектировании

Использование параболических отражателей для фокусировки света

Параболы в космическом полете

Другое применение парабол

Знаменитые параболические арки и архитекторы – Параболические арки

Нравится:

Parabola Architecture выигрывает премию AIA Leading Edge Award в области архитектуры

Добавить комментарий Отменить ответ